こんにちは、えびかずきです!
今回は最適化のテクニックを学ぼうという事で、ディープラーニングにおける様々な最適化手法を紹介したいと思います。
開発環境
OS:macOS Catalina ver10.15.2
使用した外部ライブラリ:
numpy1.18.1
matplotlib3.0.3
エディタ:jupyter notebook
ソースコード
本記事では、「#7」と「dataset」と「common」のフォルダを使用します。
最適化手法
ニューラルネットワークのパラメータどのように調整するかは、
実用的なディープラーニングを実装する上でとても重要な問題です。
既に過去記事「#5勾配法を実装しよう」で、勾配降下法を使ってパラメータを調整しましたが、
実は最適化モデルは他にも多数あります。
今回は勾配降下法の復習から初めて、その他様々は手法について紹介したいと思います。
※内容は「ゼロから作るDeepLearning」6章の内容を参考にさせていただきました。
勾配降下法(復習)とSGD
\(W ← W-η\dfrac{∂L}{∂W}\)
W:パラメータ,η:学習率,L:損失関数
勾配降下法は、損失関数(L)の勾配に応じてパラメータ(W)に修正をかけていく方法です。
勾配に応じてどれだけ調整をかけるかは学習率(η)の大きさによって決まり、その大きさをどのように設定するかは任意です。
この記事で紹介する他の手法も、この勾配降下法をベースとして作られています。
この勾配降下法に少し工夫を加えたものとして、
確率的勾配降下法(SGD:stochastic gradient descent)という手法があります。
SGDでは、学習素材全体の中からランダムに選んだミニバッチで勾配降下法を実行します。
これを繰り返すことで計算処理量を抑えつつ効率的にパラメータを最適化することができます。
勾配降下法の実装
それでは、実際に実装してみましょう!
勾配降下法は以下のようにクラスを定義することができます。
#勾配降下法(GradientDescent)
import numpy as np
class GD:
#lrは学習率を表す(learning rate)
def __init__(self, lr=0.01):
self.lr = lr
#keyは調整するパラメータを表す
def update(self, params, grads):
for key in params.keys():
params[key] -= self.lr * grads[key] 勾配降下法による学習パラメータ軌跡
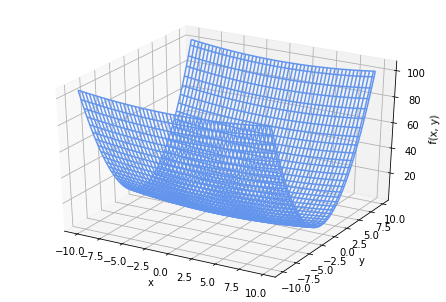
ここでは下のような関数f(x,y)を損失関数に見立てて、勾配降下法を実行してみます。
\(f(x,y)=\dfrac{1}{20}x^2+y^2\)
この関数を図示すると、下図の様になります。
x軸方向は勾配がゆるやかですがy軸方向では急、という特徴を持った関数です。
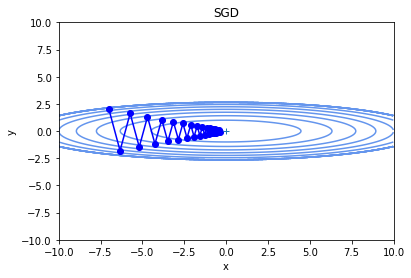
(x,y)=(-7,2)を初期値として、勾配降下法を実行した結果が下図です。
だんだん中心の最小値に近づいています。
動きに若干無駄が多いように見えますが、しっかり最適化はできています。
Momentum
続いて紹介するのが、Momentum(モメンタム)です。
momentumは運動量とか勢いという意味で、
物質の物理的な運動を参考にしてパラメータ調整に応用した手法です。
\(v ← αv-η\dfrac{∂L}{∂W}\)
\(W ← W-v\)
v:速度, α:抵抗, W:パラメータ, η:学習率, L:損失関数
momentumの実装
それでは実際に実装してみましょう。
momentumをクラスで定義した例が以下のコードになります。
#Momentum
class Momentum:
#ここではmomentumという変数がαを表す
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]
params[key] += self.v[key]momentumによる学習パラメータ軌跡
momentumで最適化を実行すると、以下のような軌跡を辿りました。
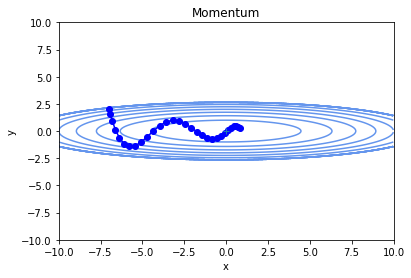
momentumだと、実際にボールが曲面上を動いているような滑かな軌跡になります。
この例の場合では、勾配降下法よりも無駄なく効率的に学習できているように見えます。
AdaGrad
AdaGradは、学習が進めば進むほどパラメータ更新の幅を小さくしていくという手法です。
“Ada”はAdapt(適応すると言う意味)を表しています。
\(h ← h+\dfrac{∂L}{∂W}\odot\dfrac{∂L}{∂W}\)
\(W ← W-η\dfrac{1}{\sqrt{h}}\dfrac{∂L}{∂W}\)
h:学習履歴, W:パラメータ,η:学習率,L:損失関数
\(\odot\)はアマダール積と呼ばれるもので、行列の要素ごとの2乗をとったものです。つまりhは学習履歴を表しており、プラス・マイナスに関わらずパラメータが大きく動けば動くほどhは大きくなっていきます。
パラメータ更新の係数には\(\dfrac{1}{\sqrt{h}}\)が使われますので、学習が進むほど、パラメータの動きは小さくなっていきます。
AdaGradの実装
Adagradをクラスとして定義した例が以下のコードです。
#AdaGrad
class AdaGrad:
def __init__(self, lr=0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)AdaGradによる学習パラメータ軌跡
Adagradで最適化を実行した軌跡が下図です。
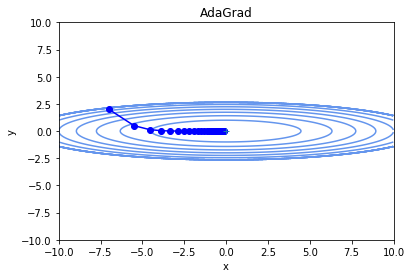
この例の場合、単純な勾配降下法だと学習の進み具合に関わらずパラメータの動きが激しく学習効率が悪かったですが、
AdaGradでは最小値に向かってきれいにパラメータが調整できています。
Adam
AdamはAdaGradとmomentumを組み合わせた最適化手法です。
ここでは具体的な理論説明は省きますが、実装のコードとパラメータ軌跡の例は以下の通りです。
AdaGradの実装
#Adam (出典:http://arxiv.org/abs/1412.6980v8)
class Adam:
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.iter = 0
self.m = None
self.v = None
def update(self, params, grads):
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)
self.iter += 1
lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)
for key in params.keys():
#self.m[key] = self.beta1*self.m[key] + (1-self.beta1)*grads[key]
#self.v[key] = self.beta2*self.v[key] + (1-self.beta2)*(grads[key]**2)
self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
#unbias_m += (1 - self.beta1) * (grads[key] - self.m[key]) # correct bias
#unbisa_b += (1 - self.beta2) * (grads[key]*grads[key] - self.v[key]) # correct bias
#params[key] += self.lr * unbias_m / (np.sqrt(unbisa_b) + 1e-7)Adamによる学習パラメータ軌跡
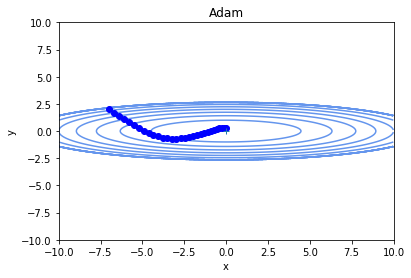
Adam,momentumの良さを活かしたきれいな曲線を描いて、最小値へ向かっていますね。
少なくとも単純な勾配降下法よりは良さそうです。
MNISTデータによる学習効率の比較
最後に「#4ニューラルネットワークを実装しよう」でも紹介した、
MNISTの手書き数字データの識別のモデルでそれぞれの最適化手法を比較してみましょう。
実際のコードはGithubのdeeplearning#4.ipynbにありますので、そちらをご参照ください。
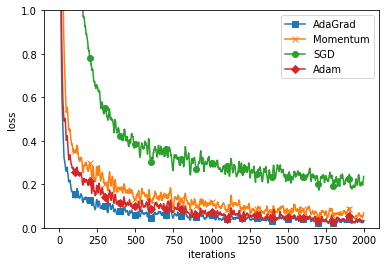
この例では、AdaGradを使うのが、最も効率が良さそうです。
とは言え単純なSGD以外の方法であればどれも学習効率は高いことが確認できます。
初期値について
最適化手法が色々あるのはわかったけど、パラメータの初期値はどうすれば良いの?
という疑問が浮かんでいる人が多いでしょう。
初期値は普通、ある程度の広がりを持ったランダムなデータを使います。
初期値なんて、何にしたって結果は同じじゃないの?
と思う方もいるかも知れませんが、そんなことはありません。
たとえば、「全部ゼロにする」だとか、「全部同じ値にする」といった初期値を与えてしまうと、
重み更新による差が生まれにくくモデルの柔軟性が失われ、最適解にたどり着きにくくなります。
と言うことで具体的にはNumpyのランダム関数を使って、
W=numpy.random.randn(n,n)*k
n:層内のノード(ニューロン )の数、k:標準偏差
のようなやり方で初期値を設定してやります。
kは標準偏差(値のばらつき具合)を決める定数で、活性化関数によってそれぞれ以下のように設定するのが良いとされています。
シグモイド関数の場合:
\(k=\sqrt{dfrac{1}{n}}\)・・・Xavierの初期値
ReLu関数の場合:
\(k=\sqrt{dfrac{2}{n}}\)・・・Heの初期値
kは小さすぎるとモデルの柔軟性が失われますし、大きすぎても、活性関数の端っこの勾配がほとんどない領域で勾配がなく値が更新されない(勾配焼失)といった、問題が生じてしまうので、注意が必要です。
バッチ正規化(Batch Normalization)
実は初期値のことをあまり考えなくても、うまく最適化を進められる手法が存在します。
それが、バッチ正規化(Batch Normalization)と言う方法です。
ここでは詳細は割愛しますが、ニューラルネット のモデルの中にデータのばらつきを整えて、
初期値にうまくばらつきを持たせてような効果をレイヤで実装するという方法です。
まとめ
今回は様々な最適化手法について紹介しました。
「勾配降下法」,「momentum」,「Adagrad」「Adam」という4つの最適化手法を紹介しました。
ここで注意したいことは、一概にどの手法が良いというものではないということです。
つまり学習モデルや初期値によって良し悪しが決まってしまうということです。
こればかりは経験によって、使う手法を見極めていく必要がありますので、
実践を重ねて感覚をつかんでいきましょう!
さて次回は、「#8過学習を回避しよう」です。
お楽しみに!
参考文献
今回記事内で使用したソースコードは「ゼロから作るDeeplearning」のものを改変して使用させていただきました。
https://www.takapy.work/entry/2018/06/13/235825
関数の3Dでのグラフ化を参考にさせていただきました。











コメントを書く