こんにちは、えびかずきです!
今回はニューラルネットワークを理解する上で欠かせない「パーセプトロン」について説明したいと思います。
※今回はPythonを使ってパーセプトロンを実装していきます。
インストール方法や使い方がわからない方は、前回の記事を参考にしてください。
パーセプトロンとは
パーセプトロンとは、人間の脳に存在して情報のやり取りをする「ニューロン」の仕組みを真似て作られた人工的な情報認識アルゴリズムのことです。
ということでまずは、脳のニューロンについて簡単に説明しておきましょう。
ニューロン

脳内のネットワークを構成する「ニューロン」は、他のニューロンからの情報を樹状突起で受けて、その入力に応じて活動電位を発生させてシナプスから他のニューロンへ情報を出力します。
人間の脳内では、このニューロンが約140億個も複雑に絡み合ってニューラルネットワークを構成することで「考える」という行為を実行していると言われています。
ディープラーニングではこの脳の仕組みを真似ることによって、コンピュータ上で人工知能を実装することができるのではないか?という発想なのです。
単純パーセプトロン(人工ニューロン)
さて本題です。ではパーセプトロンとはどういうものでしょうか?
まずは簡単な単純パーセプトロンのモデルについて説明します。
単純パーセプトロンは、ある入力の大きさが閾値以上であれば一定の出力を発するという仕組み(McCulloch-Pittsモデル)のもと作られた、単層のアルゴリズムです。
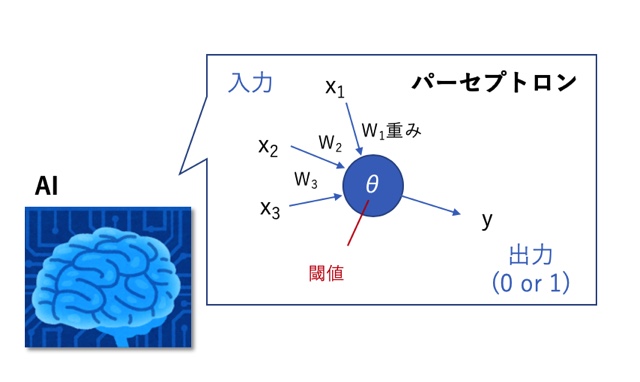
\(w_{1}x_{1}+w_{2}x_{2}\)
→θより大きいなら、y=1
→θ以下なら、y=0
McCulloch-Pittsモデルとは重み付きの入力の総和が閾値より大きければ「1」を、閾値以下であれば「0」を出力するのというモデルです。
例えば、上の図のようにx1,x2という入力が単純パーセプトロンに入った場合、それぞれに重みをかけて足した数値が閾値(θ)より大きいか、そうでないかによって出力が決まるのです。
単純パーセプトロンは非常に単純な構造ですが、これを組み合わせてネットワーク構造を形成することによって、様々な出力を表現することができるようになるのです(これを実感できるのはもう少し後になりますが)。
パーセプトロンを実装してみよう
それでは、実際にパーセプトロンを実装してみましょう。
ここで紹介するソースコードはGithub上に保存していますので、ダウンロードして使ってください。
開発環境
OS:macOS Catalina ver10.15.2
使用した外部ライブラリ:
numpy1.18.1
エディタ:jupyter notebook
ソースコード
github/ebikazuki/deeplearning
→本記事のコードは#2のフォルダです。
2入力の単純パーセプトロン
上の図で説明した、入力データが2つある時の単純パーセプトロンを実際に作ってみましょう。
※説明はコード内にコメントアウト(#)で記載していますので参考にしてください。
#2入力の単純パーセプトロン
#numpy配列(array)を使うためにnumpyをインポートする
#as npとすることで、クラス名を”np”と省略して使えるようになる
import numpy as np
#入力xを配列として定義,数値はそれぞれx1,x2を表す
x = np.array([0.6, 0.8])
#重みwを配列として定義,数値はそれぞれw1,w2を表す
w = np.array([0.5, 0.5])
#閾値θを定義
theta = 0.5
#出力yをif文で判定する
if np.sum(w*x) > theta :
y = 1
else:
y = 0
#結果を表示する。\nは改行コード
print('[x1 x2]=',str(x),'\ny=',str(y))実行結果:
[x1 x2]= [0.6 0.8] y= 1
入力としてx1=0.6,x2=0.8、重みとしてw1=0.5,w2=0.5、閾値としてθ=0.5と設定すると、期待通りy=1が出力されました。
これでディープラーニング学習の入り口とも言える、単純パーセプトロンが実装できました!
論理回路を作ってみよう
上の簡単な例だけではちょっと物足りないので、応用として単純な論理回路をパーセプトロンを使って作ってみましょう。
論理回路は、我々の持っているコンピュータがあらゆる計算を実行するための基本構造です。これらの組み合わせによって足し算や掛け算、はたまたプログラムされたアルゴリズムなどあらゆる処理を実行できます。
つまりこれらの回路を作ることができれば、原理的にはパソコンと同じ計算ができるということの証明になるのです。
ここでは、論理回路としてANDゲート、NANDゲート、ORゲートを作ってみましょう!
ANDゲート
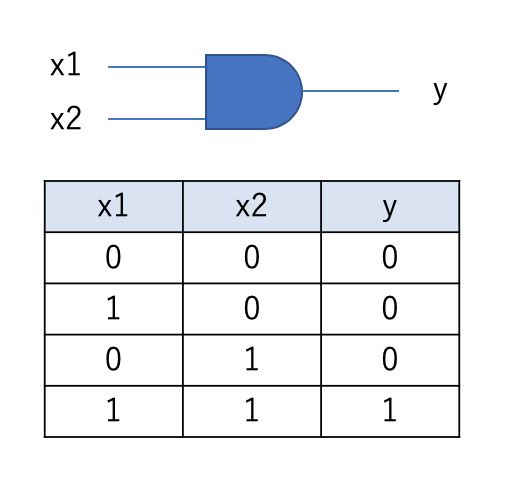
#ANDゲート
import numpy as np
#関数を定義する、returnは戻り値(関数の出力)の指定
def AND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
theta = 0.8
if np.sum(w*x) > theta :
return 1
else:
return 0
if __name__ == '__main__':
for x in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = AND(x[0], x[1])
print(str(x) + " -> " + str(y))実行結果:
(0, 0) -> 0 (1, 0) -> 0 (0, 1) -> 0 (1, 1) -> 1
if __name__ == ‘__main__’:について
コード例の中のこの記述は、もしこのプログラムがメインで実行された場合に実行されるif文となります。
つまり、上のANDゲートの例の場合、このプログラムをメインで実行した場合には入力と出力の全セットが参考として表示されるというコードになっています。
この関数を他のプログラムから呼び出して使用することも考慮して、こういう記述にしています。(関数を呼び出して使うときにいちいち入出力例を表示されると目障りですからね。)
NANDゲート
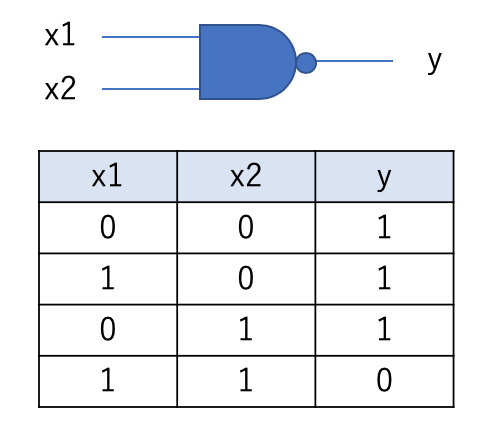
#NANDゲート
import numpy as np
def NAND(x1, x2):
x = np.array([x1, x2])
w = np.array([-0.5, -0.5])
theta = -0.8
if np.sum(w*x) > theta :
return 1
else:
return 0
if __name__ == '__main__':
for x in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = NAND(x[0], x[1])
print(str(x) + " -> " + str(y))実行結果:
(0, 0) -> 1 (1, 0) -> 1 (0, 1) -> 1 (1, 1) -> 0
ORゲート
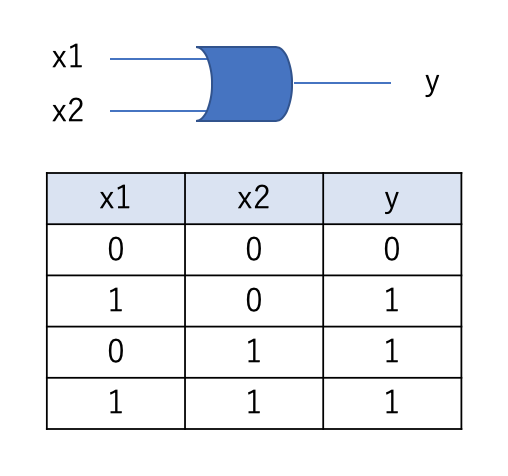
#ORゲート
import numpy as np
def OR(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
theta = 0.2
if np.sum(w*x) > theta :
return 1
else:
return 0
if __name__ == '__main__':
for x in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = OR(x[0], x[1])
print(str(x) + " -> " + str(y))実行結果:
(0, 0) -> 0 (1, 0) -> 1 (0, 1) -> 1 (1, 1) -> 0
適切に重みと閾値を設定することによって、論理ゲートを作れることがわかりましたね。
本当にパーセプトロンでいろんな表現ができるか?
ここまでの説明では、例が単純過ぎてパーセプトロンで本当に複雑な計算ができるという実感が湧かないと思います。
ここではちょっと難しいですが、なるべく噛み砕いて線形性と非線型性という概念について説明をしておこうと思います。
線形性と非線形性
例えば、上で紹介したAND、NAND、ORゲートは線形性を持っています。
重み付きの和から出力の0or1を判断するというのは、図示するとちょうど下図のようになります。
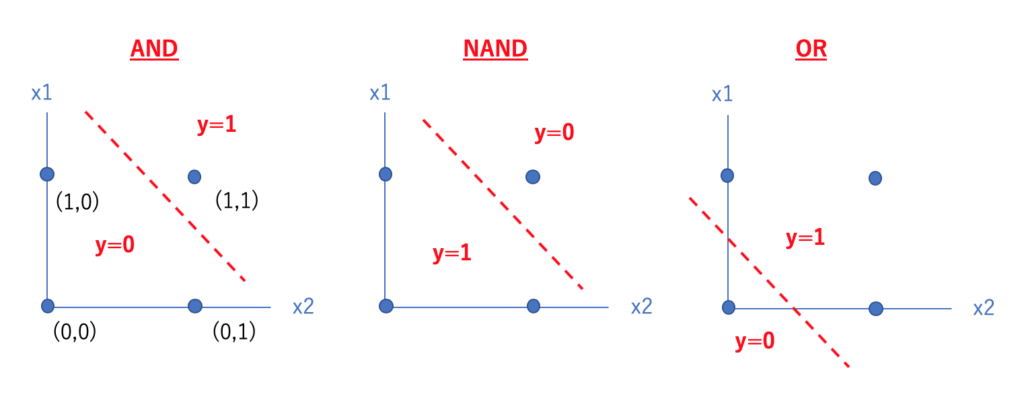
すなわち、x1,x2を軸とするグラフ上に適切な直線を一本だけ引いて領域を分けることで、出力を調整しています。
しかし、これだと複雑な分類はできていません。
たとえば、非線型性をもつXOR(排他的論理和:2進数の足し算の繰り上げをするときに必要な論理回路)を考えてみましょう。
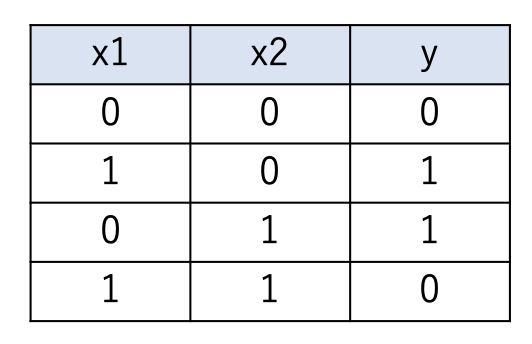
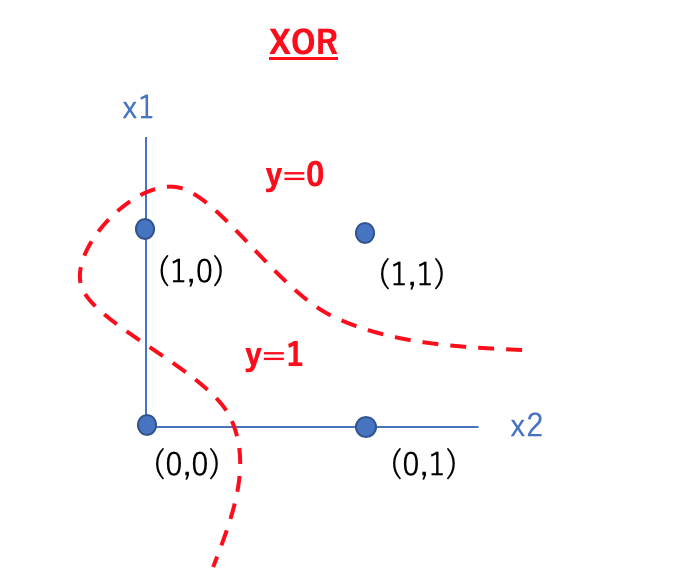
この場合、一本の直線で領域を分けて、XORを表現することが出来ません。すなわちXORゲートは非線型性なのです。
ではどうすれば非線型性を有する問題を解決できるでしょうか?
XORゲートの作り方(多層パーセプトロン)
実はXORゲートはAND、NAND、ORゲート(単純パーセプトロン)を組み合わせることによって作ることが出来ます。
つまり、単純パーセプトロンを組み合わせて多層パーセプトロンとすることで非線型性を表現できるようになるのです!

組み合わせて作るというのは、結局領域を分ける直線を増やしたということになります。
これによって表現力が増し、一本の直線だけで分けるという線形性から脱することが出来るのです!
ここでやっていることは、下のようにORとNANDの2本の線で領域を3つに分けて、ANDで真ん中の領域がy=1になるように閾値を設定しているということなのです。
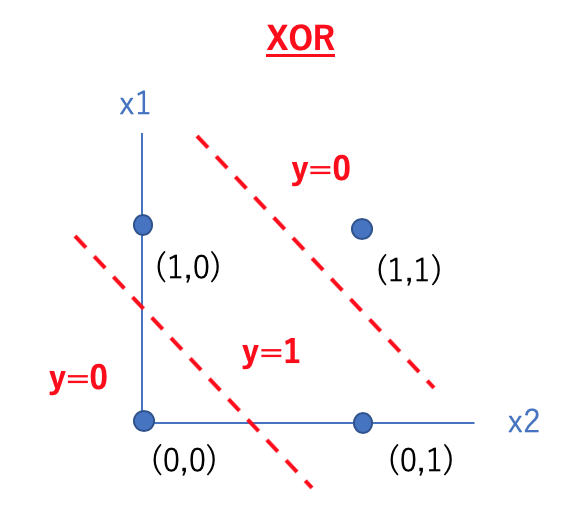
ではプログラムを書いて実装してみましょう!
既に定義したAND,NAND,OR関数を呼び出してXORゲートを作成します。
#XORゲート
def XOR(x1, x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y
if __name__ == '__main__':
for x in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = XOR(x[0], x[1])
print(str(x) + " -> " + str(y))XORゲートでもまだ単純ではありますが、単純なパーセプトロンを組み合わせて多層パーセプトロンを構成することによって、非線型の問題にも対応できるということがわかったと思います。
さらに複雑な非線型問題があったとしても、たくさんの直線を使って領域を分けてやれば良いということです。
まとめ
今回はディープラーニングを学ぶために欠かせない、パーセプトロンという基本の考え方について説明しました。
上で紹介した通り、とても簡単な単純パーセプトロンを組み合わせることによって、複雑な計算を実行できるということを示しました。
あとは如何にうまく組み合わせ、最適な構造や重みなどのパラメータを学習させるかという問題になってきます。
ようやくディープラーニングっぽくなってきました。
次回は活性化関数についてです!
乞うご期待!
参考書籍
今回記事内で使用したソースコードは「ゼロから作るDeeplearning」のものを改変して使用させていただきました。












コメントを書く