
こんにちは、えびかずきです!
今回は「過学習を回避しよう」です。
この記事ではニューラルネットで過学習を防ぐ方法として、
Weight DecayとDropoutの2つを紹介したいと思います!
開発環境
OS:macOS Catalina ver10.15.2
使用した外部ライブラリ:
numpy1.18.1
matplotlib3.0.3
エディタ:jupyter notebook
ソースコード
本記事では、「#8」と「dataset」と「common」のフォルダを使用します。
過学習とは?
過学習(Over Fitting)とは、
モデルが訓練データに悪い意味でフィットし過ぎてしまって
新しいデータに対する整合性がとれなくなってしまう現象のことを言います。
過学習が起きやすい条件は以下の二つです。
・モデルの表現力が高い
・訓練データ数が少ない
モデルの表現力が高いことがディープラーニングの良い面でもある訳ですが、
下手に使うと過学習で実用性がなくなってしまうという事です。
過学習の例
たとえば下の例を見てください。
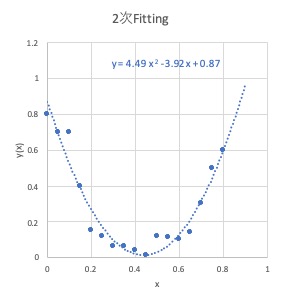
これは、相関のあるxとyというデータを、関数y(x)で最小二乗法フィッティングした結果です。
2次関数の方(左)は、
データを滑らかにフィッティングできています。
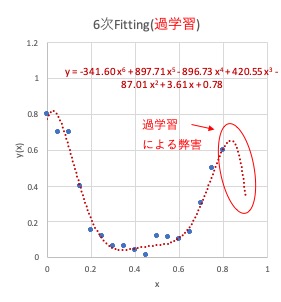
一方の6次関数(右)は
ややいびつで、データのない外側の領域はおかしな曲線になってしまっています。
このような状態が過学習です。
モデルの表現力が高いために訓練データとの差は小さいのですが、
訓練データのない外側の領域ではモデルの複雑性を引き継いでしまって
実用的なフィッティングとは言えません。
ではこれを回避するテクニックを紹介していきましょう!
過学習を防ぐテクニック
Weight Decay
Weight Decay(直訳すると荷重減衰)とは、
重みのパラメータが大きくなり過ぎないように制限をかけることで過学習を防ぐ方法です。
これは機械学習の世界で正則化と呼ばれる手法になります。
過学習が起きてしまう典型的なケースとしては、
たくさんの変数で訓練データを説明してしまって訓練後のモデルが複雑化してしまうというケースです。
ちょうど上の「過学習とは?」で説明した6次関数のように、
たくさんの変数で訓練データをフィッティングしているようなケースです。
こういったケースでは、重みの2乗の総和が大きくなっています。
例えば、上の2次関数と6次関数の例で比較してみると、
重みの二乗の総和の比較:
・2次関数:36.28
・6次関数:1911145.18
と、圧倒的に6次関数の場合の方が大きくなっています。
Weight Decayではこの重みの二乗の総和を損失関数に加えることで、
過学習を防ぎます。
すなわち重みが大きくなることに制限をかけるという事です。
\(L=E+\dfrac{1}{2}λ\sum_k{(w_k)^2}\)
L:損失関数、E:誤差関数、λ:正則化パラメータ、W:重み
具体的には上式のように、誤差関数に重みの二乗の総和を加えたものを損失関数として、
ニューラルネットの学習を実行します。
λは正則化パラメータといって、正則化の強さを調整するパラメータです。
係数の1/2は、勾配逆伝播法で微分して勾配に変換した時に、
係数が消えてλwという簡単な項を導くための、テクニカルな工夫です。
ちょっと感覚的な説明になってしまいましたが、
詳しく原理を理解したい場合はL2正則化やRidge回帰で調べると意味や原理を詳しく知る事ができます。
用語に関する筆者のぼやき:
Weight Decay-荷重減衰は、個人的には荷重抑制の方が内容的にしっくり来る。
別に重みが減衰していく訳ではないので、なんだかイメージが違うように思います。
一方Regularization-正則化は、個人的には適正化とかの方がしっくり来る。
正則化というと何か規則みたいなものに合わせるというようなニュアンスを感じますが、実際は適切な方向に寄せるというような手法だと思います。
英語から日本語に変換して名前が付いたんだろうけど、呼び方を変えたいです。
Weight Decayの効果確認
それでは、Weight Decayの効果を確認してみましょう!
今回もMNISTの手書き文字データを使っていきます。
学習条件は以下の通りです。
入力:
訓練データ:100個
テストデータ:100個
モデル:
入力層(784)
隠れ層1~6(100)
出力層(10)
活性化関数:ReLu
最適化:SGD(η=0.01)
Weight Decay-λ:0.05
学習:
バッチ:100
エポック:200
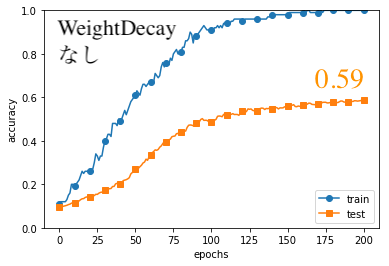
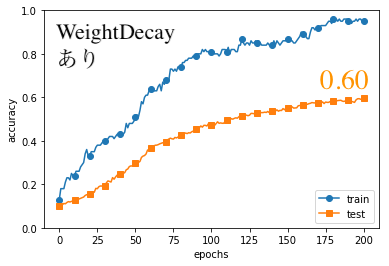
結果は以下の通りになりました。(コードはGithubの「#8」フォルダ)
testの方の結果を見てみると、
わずかにWeightDecayありの方が、よい結果となりました。
注目すべきは、WeightDecayありのtrain(訓練)データの精度が1.0になっていないという点です。
これが過学習を回避できている証拠です。
Dropout
Dropoutとは、
学習実行時にニューラルネットワーク内のノード(ニューロン )をバッチ毎にランダムに消してしまうことで、過学習を防ぐテクニックです。
イメージとしては下図の通りです。
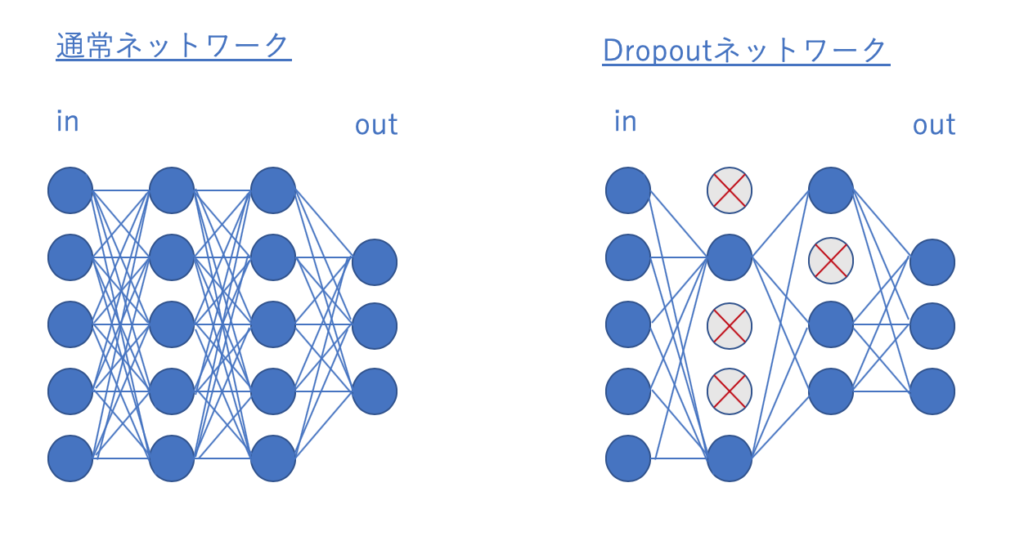
一つのバッチで学習が終われば、次のバッチではまた違う箇所を消してやって学習をすすめます。
なぜこれで過学習を防げるかというと、モデルの複雑化を防ぐことができるからです。
モデルが複雑になって、冒頭説明したような6次関数のようなフィッティングになっていると、ある次元を一つ減らすと、モデルが大きな影響を受けて乱れてしまいます。
こういうロバストネス(外乱に対する強さ)の低い複雑なモデルになってしまわないように、
Dropoutでモデルを単純化しつつ学習を進めることで、モデルの柔軟性は保ちつつ、過学習を回避できるというわけです。
実際に実装する際には、Dropout率(0~1)を定めて、バッチ毎の学習を進めます。
Dropoutの効果確認
ここでもMNISTの手書き画像データで効果を確認してみましょう!
学習条件は以下の通りです。
入力:
訓練データ:100個
テストデータ:100個
モデル:
入力層(784)
隠れ層1~6(100)
出力層(10)
活性化関数:ReLu
最適化:SGD(η=0.01)
Dropout_ratio:0.02
学習:
バッチ:100
エポック:200
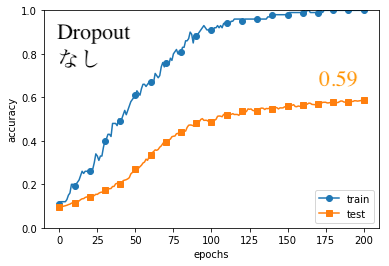
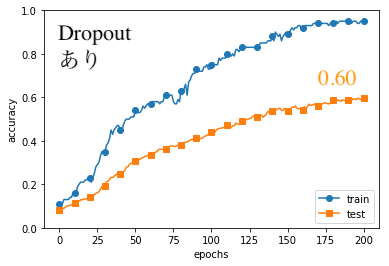
結果は以下の通りになりました。(コードはGithubの「#8」フォルダ)
こちらもtestの方を見てみるとWeight Decayの時と同様に、対策を講じたDropoutありの方が、わずかに良い結果となりました。
やはり訓練データの精度は1.0には達しておらず、過学習が回避されています。
まとめ
ということで今回は過学習を回避するためのテクニックについて説明しました。
これまでスイスイと学習を進めて来ましたが、
今回の「WeightDecay」や「Dropout」といった考え方は、初心者にとって少しわかりづらい概念かと思います。
でもここを乗り越えられるかどうかが、初心者と中級者の分かれ道です。
しっかり学習して、ディープラーニングを自分のモノにしましょう!
次回はいよいよCNN(Convolutional Neural Network)で画像分類をします。
お楽しみ!
参考書籍
今回記事内で使用したソースコードは「ゼロから作るDeeplearning」のもの
改変して使用させていただきました。












コメントを書く