
こんにちは、えびかずきです!
前回までにニューラルネットワークの基礎的な原理は一通り説明しましたので、
この記事からは実用的に使うためのテクニックを説明していきます!
誤差逆伝播法とは何か
誤差逆伝播(ごさぎゃくでんぱ)法とは、勾配を効率的に求めるためのテクニックです。
back-propagation(バックプロパゲーション)とも呼ばれます。
前回の勾配法では、損失関数を重みやバイアスで数値的に微分をして勾配を求めましたが、
実はもっと効率のよいやり方があります。それがこれから説明する誤差逆伝播法です。
誤差逆伝播法は簡単に説明すると以下2点に集約されます。
①解析的な微分を使う(数値演算量が軽減される)
②連鎖律に従って微分を逆から辿る(演算の重複が無くなる)
微分をきちんと理解している人にとっては、とても簡単なことですぐに理解できると思いますが、
第0回の記事で中学生でも理解できる程度に説明すると言ってしまったので、
なるべくきちんと説明したいと思います。
もしかしたら微分をよくわかっている人上の①、②を読むだけで中身はある程度予想できるかも知れません。
※微分自体の概念は前回の記事を参考にしてください。
ここではその続きとして連鎖律の話をします。
数値的な勾配算出(前回の復習)
前回の記事では、数値的に勾配を算出して勾配法を実装しました。
例えば、下のようなモデルで誤差関数Lの重みw1,w2に関する勾配を求めることを考えます。
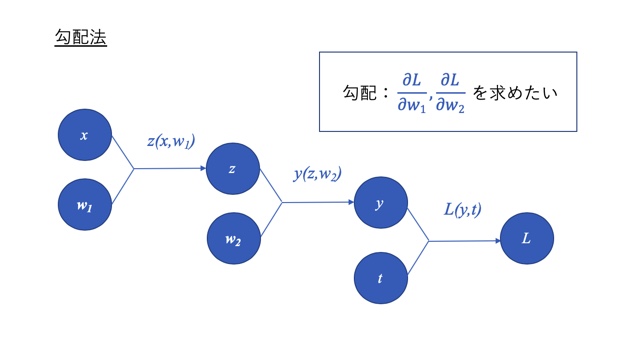
数値的な勾配法の場合は、下図のように微分の定義式を少し修正した形で、
微小幅hにはたとえば10e-4などの小さい数値を代入して勾配を求めました。
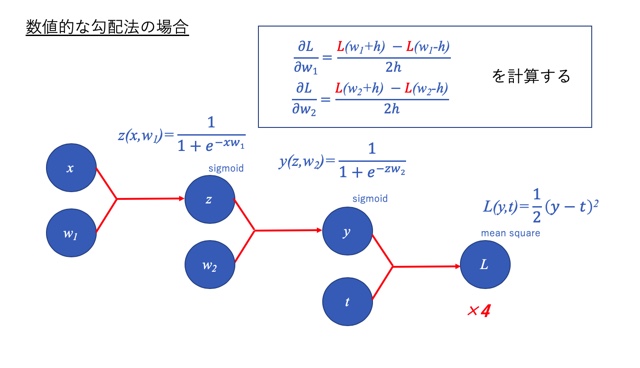
しかし、これは計算量がかなり多く、実は無駄の多い方法なのです。
計算式中に赤で示したLの面倒な計算が4回も入っています。
これくらいの小さなネットワークであれば特に計算量を気にする必要はないですが、
実用的なもっと複雑なモデルでディープラーニングを実装することを想定すると、
極力無駄は省かなければなりません。
では、どうすれば良いでしょうか?
その答えの一つは解析的な微分を使うということです!
解析的な勾配算出
解析的な微分とは、これまでのように微小幅hに小さい数を入れて数値的に解くのではなく、
微分の定義に従って極限の計算を解析的に実施するということです。
解析的な微分
例えば\(f(x)=x^2\)という関数があるとしましょう。
この関数の微分は、定義に従うと下のような式になります。
\(\dfrac{df(x)}{dx}=2x\)
このように関数を解析的に微分を実施しておいて、
あとはコンピュータに数値計算をさせるだけという準備をしておくというやり方です。
解析的な微分の計算はある程度の訓練が必要です。
その法則とテクニックに慣れれてしまえば簡単です。
高校生以上の方は既に学校で習っていると思いますが、
中学生以下の方は高校数学を予習してみても良いでしょう。
但しあまりここでハマりすぎると次に進めないので、
結果だけ受け入れて次に進んでも、ディープラーニングの本質的な理解には差し支えないでしょう。
解析的な勾配算出の例
例えば、上の例と同じモデルで勾配を求める場合を考えてみましょう。
ここでは微分計算の過程は数式ばかりで嫌になると思うので示しませんが、
結果だけ下図に示しました。
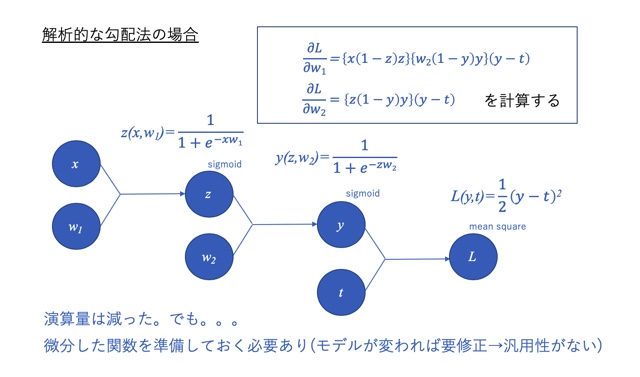
得られる勾配は、図中右上の枠内の式になります。
一見複雑にも見えますが、数値的な勾配算出で誤差関数Lを4回も計算していたのと比べると、計算量は半分くらいに減っています。
しかし、これでめでたしめでたしという訳ではありません。
このやり方には問題があります。
それはモデルが変わると微分の関数を修正しなければいけないということです。
さらに言えば、モデルが複雑になると、微分の計算を間違える恐れがあるということです。
これでは実用性がありません。
そこで微分の連鎖律を考えます。
微分の連鎖律について
微分の連鎖律とは、
下図のとおり、分数の掛け算の演算のように分母と分子が同じなら消せるという法則のことです。

これはとても便利な法則です。
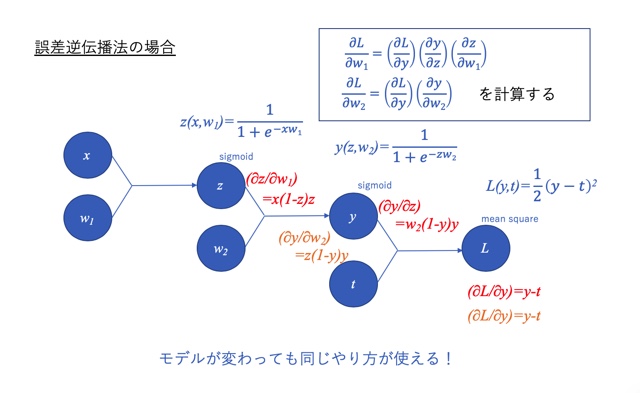
なぜなら、今考えているモデルに当てはめると、図中右上の枠の関係が成り立ち、
それぞれの関数の偏微分を求めて、後で組み合わせれば良いからです。
これならモデルが変わったとしても、それぞれの関係を個別に求めれば良いのでの汎用性があり、使いやすさがグッと増しました。
実際には、それぞれの偏微分を右から左に向かって計算して、組み合わせて行きます。
この計算の方向が逆順になっていることが、「誤差逆伝播法」と呼ばれる理由です。
この方向で計算を実行することによって無駄な計算をせずに済みますし、計算の重複も回避できます。例えば上の例では∂L/∂yがw1,w2どちらにも現れますが、右から順番に計算していくというやり方なら重複しません。
レイヤについて
誤差逆伝播法の理論がわかったところで、実装に向けてレイヤという概念を説明しておこうと思います。
ニューラルネットワークでは下図のようにネットワークを層状に重ねてモデルを作りました。
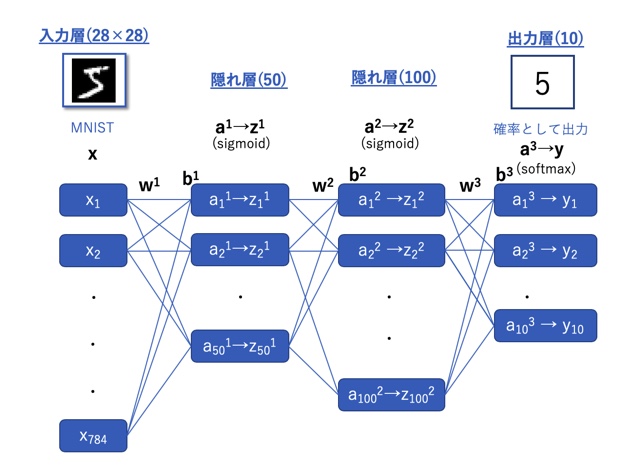
レイヤ(層)は文字通り層を意味する単語ですが、
ここでは前の層からきた情報を処理するプログラム上の関数を意味し、行列を受け渡しを行います。
レイヤは下図のように、順(右)方向のテスト演算と、
逆(左)方向の逆伝播による勾配演算を含みます。
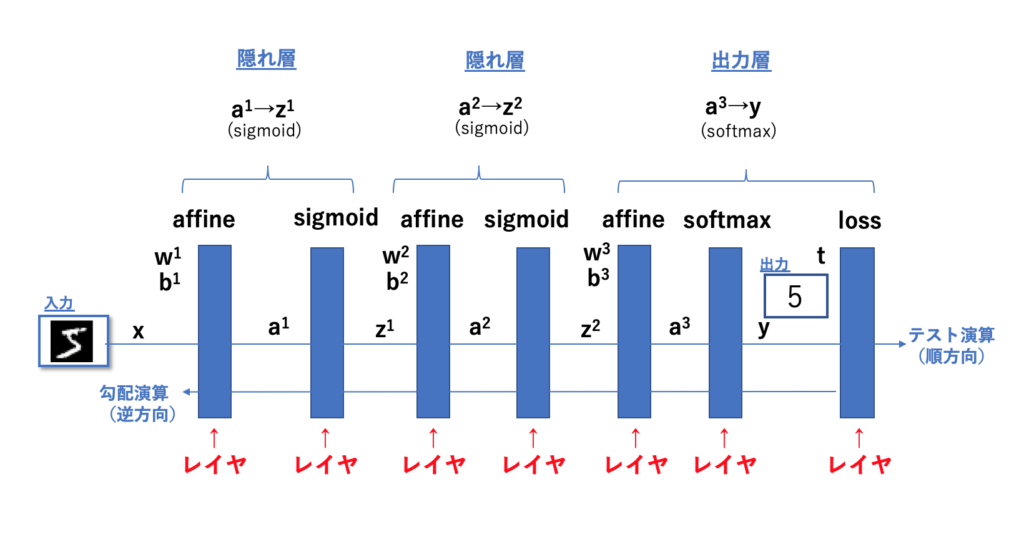
実は既に順方向のテスト演算については前回までの記事にて説明済みです。
具体的には、行列の積や活性化関数そして誤差関数などのことです。
これに勾配を算出するための逆方向演算の関数を定義すればレイヤが完成というわけです。
このようにレイヤという形でニューラルネット内の演算を層状にまとめてやることで、モデルの組み立てがとても容易になります。組みたいモデルに応じてレイヤ(pythonで定義する関数)を入れたり抜いたりすれば良いだけですからね。
開発環境
誤差逆伝播の原理がわかったところで、ニューラルネットワークへの実装を考えていきましょう!
本記事のコードは以下の環境で動作することを確認しています。
OS:macOS Catalina ver10.15.2
使用した外部ライブラリ:
numpy1.18.1
matplotlib3.0.3
エディタ:jupyter notebook
ソースコード
github/ebikazuki/deeplearning
本記事では、「#6」と「dataset」と「common」のフォルダを使用します。
活性化関数レイヤの実装
それぞれのレイヤをクラスで定義したコード例です。
順方向については過去記事で紹介しましたが、ここでは逆方向の逆伝播の演算も含めてレイヤとして定義します。
Sigmoidレイヤ
#sigmoidレイヤの実装
import numpy as np
from common.functions import *
class Sigmoid:
def __init__(self):
self.out = None
def forward(self, x):
out = sigmoid(x)
self.out = out
return out
def backward(self, dout):
dx = dout * (1.0 - self.out) * self.out
return dxReLUレイヤ
#ReLUレイヤの実装
import numpy as np
from common.functions import *
class Relu:
def __init__(self):
self.mask = None
def forward(self, x):
self.mask = (x <= 0)
out = x.copy()
out[self.mask] = 0
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout
return dxAffineレイヤの実装
Affineレイヤは行列演算のレイヤのことです。
順方向については、これまでnp.dot()で処理してきた行列の積を適用すればOKです。
そこに逆方向の演算を追加してAffineレイヤのクラスとして定義します。
#Affineレイヤの実装
import numpy as np
from common.functions import *
class Affine:
def __init__(self, W, b):
self.W = W
self.b = b
self.x = None
self.original_x_shape = None
# 重み・バイアスパラメータの微分
self.dW = None
self.db = None
def forward(self, x):
# テンソル対応
self.original_x_shape = x.shape
x = x.reshape(x.shape[0], -1)
self.x = x
out = np.dot(self.x, self.W) + self.b
return out
def backward(self, dout):
dx = np.dot(dout, self.W.T)
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
dx = dx.reshape(*self.original_x_shape) # 入力データの形状に戻す(テンソル対応)
return dxSoftmax with Lossレイヤ
最後にSoftmax with Lossレイヤです。
ここではSoftmax関数とクロスエントロピー誤差関数をまとめて一つのレイヤとして定義します。
#Softmax-Lossレイヤの実装
import numpy as np
from common.functions import *
class SoftmaxWithLoss:
def __init__(self):
self.loss = None
self.y = None # softmaxの出力
self.t = None # 教師データ
def forward(self, x, t):
self.t = t
self.y = softmax(x)
self.loss = cross_entropy_error(self.y, self.t)
return self.loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
if self.t.size == self.y.size: # 教師データがone-hot-vectorの場合
dx = (self.y - self.t) / batch_size
else:
dx = self.y.copy()
dx[np.arange(batch_size), self.t] -= 1
dx = dx / batch_size
return dx誤差逆伝播法の実装
ではレイヤを使って実際にニューラルネットのモデルを組んでみましょう!
今回もMNISTの手書き数字の画像サンプルを使って、画像の数字を認識するプログラムを組んでいきます。
コードは、Githubリポジトリ(github/ebikazuki/deeplearning)の
「#6」のフォルダ中にあるdeep learning#6.ipynbを使います。
モデル条件:
ネットワーク:Affine(50)-ReLU-Affine(10)-Softmax with Loss
訓練データ:MNIST-60,000枚(28×28ピクセル)
テストデータ:MNIST-10,000枚(28×28ピクセル)
最適化:勾配降下法(学習率=0.1)
バッチサイズ:100
演算回数:10,000回(約17epoch)
この中にプログラムが二つあり
「#レイヤで実装したニューラルネットワーク」にネットワークのクラス定義が、
「#訓練」に訓練を実行するコードを記述しています。
順番に実行してモデル学習を試してみてください!
出力:
0.1092 0.109 0.9019333333333334 0.9061 0.9223833333333333 0.9238 0.9352833333333334 0.9358 0.9435 0.9427 0.9521666666666667 0.9498 0.9568166666666666 0.9543 0.95975 0.9554 0.9643333333333334 0.9608 0.9677333333333333 0.9633 0.9691833333333333 0.9647 0.9717833333333333 0.9671 0.9726 0.9665 0.9745666666666667 0.9693 0.9762333333333333 0.9686 0.9768166666666667 0.9677 0.9779166666666667 0.9694
出力として、エポックごとに訓練データの精度とテストデータの精度が表示されています。
いずれも訓練が進むにつれて精度が増していて、
きちんとニューラルネットでもモデル学習が進んでいることが確認できました!
まとめ
今回は誤差逆伝播法について説明しました。
微分に慣れていない方にとっては少し苦しい回だったかも知れませんが、いかがだったでしょうか。
とはいえ仕組み自体はとても単純で
誤差逆伝播を簡単に言えば、
微分の連鎖律を使って逆順で解析的に勾配を求めるということです。
次回は、「最適化のテクニックを学ぼう」と言うことで、勾配法の種類や、その他のパラメータ調整方法について説明したいと思います。
例えば、SGD、Momentum,Adagrad,Adamなどが登場します。
乞うご期待!
参考書籍
今回記事内で使用したソースコードは「ゼロから作るDeeplearning」のものを改変して使用させていただきました。











[…] 第5回:勾配法を実装しよう 第6回:誤差逆伝播法を実装しよう 第7回:最適化のテクニックを学ぼう 第8回:過学習を回避しよう […]