こんにちは、えびかずきです。
今回はベイズ分類規則の原理についてはじパタ3章の前半を読み進めた記録を残しておきます。
こんな人におすすめ:
・ナイーブベイズの実装方法についてPythonで学びたい
・機械学習の入門で「はじパタ」を読んでいるが難しいので解説して欲しい
機械学習の理論的理解のために、最近「はじめてのパターン認識」を読んでいます。
Pythonユーザーである私は、プログラムを書きながら具体的に理解していくという方法をとっっているので、その記録を残しておこうと思います。
ということで今回は、はじパタ3章をPythonで実装しながら読み進めた記録です。
読んでくれた方の理解の手助けとなれば幸いです。
開発環境
Python 3.7.3
scikit-learn 0.24.2
NumPy 1.20.2
エディタ:jupyter Notebook
ベイズ分類規則とは
ベイス分類規則は確率分布を仮定したクラス分けの分類手法です。
特に、はじパタ3.1.2(第1版p23)に記載の特徴量の条件付き独立を仮定したモデルは、ナイーブベイズ(単純ベイズ)と呼ばれる最も基本的な分類手法の一つ。
機械学習入門においてこの原理は実用上はもちろんのこと、機械学習の歴史的な文脈を理解するためにも知っておいた方が良いです。
ナイーブベイズを含むベイズ分類規則は、高速なデータ処理が期待される手法であるため、膨大なデータの分類に威力を発揮すると言われています。
しかし一方で分類精度を追い求める場合には、他の手法(例えばSVMなど)を使った方が良い場合が多く、最近は新しい分類手法のベンチマークとして負けるべき比較対象として選ばれる例が多いようです。
ベイズ分類規則の原理
ベイズ分類規則は、ご存知の通りベイズの定理を使った分類手法です。
ベイズの定理:
\(\rm P(C_i|\bf x \rm )=\dfrac{p(\bf x\rm |C_i)}{p(\bf x \rm )}×P(C_i)\)
\(\rm P(C_i|\bf x \rm ):事後確率\)
\(p(\bf x\rm |C_i):尤度\)
\(p(\bf x \rm ):周辺確率\)
\(P(C_i):事前確率\)
ベイズ分類規則というのは、この事後確率が最大になるようにクラス分類をする方法のことを言います。
といっても抽象的すぎて理解しにくいと思うので、ここからは具体的な例をあげて説明していきます。
ちなみに「はじパタ」の中では『ある町の喫煙と飲酒に関するデータ』を使った尤度がベルヌーイ分布となる具体例で説明しています。
それと同じでは芸がありませんので、ここでは尤度がガウス分布(正規分布)になっているような例で説明します。
具体的な活用例
尤度がガウス分布の問題例「健康診断の分析」:
会社で実施した健康診断のデータがここに1000人分ある。
検査で肝臓が弱っていることを示すγGTPの値が基準値を超えた人を1、超えなかった人を0と分類するデータを得ている。
さらに検査と同時にアンケートを実施しており、1週間の飲酒量がアルコール換算で何mLかというデータも取得している。
1と分類された人は200人で飲酒量の分布は、平均=200mL、分散=50mLのガウス分布、
0と分類された人は800人で飲酒量の分布は、平均=80mL、分散=40mLのガウス分布、
で近似できる時、1週間の飲酒量が150mLの人は1,0のどちらに分類するのが妥当か?
ここでは、クラスを表す変数をCとして0と1を取り、特徴量データが一つだけなので、xは1次元のベクトル(つまりスカラー)で飲酒量を表すこととします。
この時、考えるベイズの定理は、
\(P(C=1|x=150)=\dfrac{p(150|C=1)}{p(x=150)}×P(C=1)\)
\(P(C=0|x=150)=\dfrac{p(150|C=0)}{p(x=150)}×P(C=0)\)
この二つです。
あとは、このうちどちらの事後確率が大きいかを比較して、大きい方のクラスに分類すれば良いというわけです。
それでは式を計算していきましょう。
まず事前確率は、
\(P(C=1)=200/1000=0.2\)
\(P(C=0)=800/1000=0.8\)
つづいて尤度については、正規分布で考えているので、
\(p(150|C=1)=N(x=150,μ=200,σ^2=50)=0.00484\)
\(p(150|C=0)=N(x=150,μ=80,σ^2=40)=0.00216\)
ここでNは正規分布関数を表す
最後に周辺確率は、クラスごとの同時確率の和を計算すれば良いので、
\(p(x)=p(C_1,x)+p(C_0,x)\)
\(=P(C_1)P(x|C_1)+P(C_0)P(x|C_0)\)
\(=0.2N(μ=200,σ^2=50)+0.8N(μ=80,σ^2=40)\)
となって、
ここにx=150を代入すれば良いので、
\(p(x=150)=0.2N(x=150,μ=150,σ^2=50)+0.8N(x=150,μ=80,σ^2=40)\)
\(=0.2p(150|C=1)+0.8p(150|C=0)=0.00269\)
となる。
よってそれぞれの事後確率を計算すると、
\(P(C=1|x=150)=0.36\)
\(P(C=0|x=150)=0.64\)
となる。
計算の結果、\(P(C=0|x=100)>P(C=1|x=100)\)ということがわかったので、
今回のケースでは、C=0つまり健康診断で引っかからない方へ分類するのが妥当と言えます。
実際は周辺確率p(x=100)の計算はクラス分類には必要ないのですが、今回は理解を深めるために一応計算しておきました。
視覚的な説明
数式だけだとわかりづらいので、Pythonで上の例を図示してみました。
ベイズ分類では結局のところ、それぞれのクラスで\(p(x|C_i)P(C_i)\)という関数を考えて、xに具体的な数値を代入した時に大きくなる方を選べば良いので、
それを図示すると、こうなります。
from matplotlib import pyplot as plt
x = np.arange(start = 0, stop = 400, step = 1)
plt.plot(x, 0.2*stats.norm.pdf(x=x, loc=200, scale=50), label='クラス1')
plt.plot(x, 0.8*stats.norm.pdf(x=x, loc=80, scale=80), label='クラス0')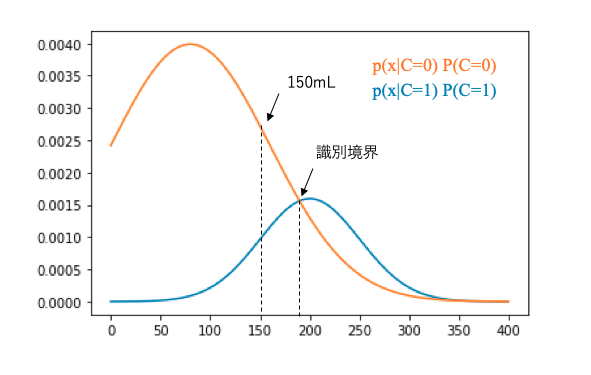
こうやって図示してみると、数式で考えていた時よりだいぶ見やすくなりましたね。
図示すると識別境界がどこにあるかもわかりやすくなります。
今回のケースでは識別境界が190mL付近にあることが読み取れます。
scikit-learnによる実装例
ここでは、はじパタ3.1.2(第1版p23)に例示されている、『ある町の喫煙と飲酒に関するデータ』の分析をPythonで実装してみました。
ここでの分類規則はナイーブベイズに該当する手法ですが、Pythonの場合、scikit-learnのnaive_bayesメソッドで実装することができます。
はじパタの例示をPythonで分析した例を下に示します。
#2章の実装
from sklearn.naive_bayes import BernoulliNB
import numpy as np
# データの生成
S = [1]*480+[0]*(1000-480)
G = [1]*320+[0]*160+[1]*480+[0]*40
for i , x in enumerate(np.argsort(G)):
if i < 160:
T[x] = 0
elif i < 200:
T[x] = 1
elif i < 360:
T[x] = 0
else:
T[x] = 1
S = np.array(S).reshape(-1,1)
T = np.array(T).reshape(-1,1)
X = np.concatenate([S, T], 1)
Y = np.array(G)
# モデル作成
model = BernoulliNB()
clf = model.fit(X,Y)
# 分類結果
print(clf.predict([[0,0],[0,1],[1,0],[1,1]]))
# OUTPUT:
# [1,1,0,1]アウトプットを見てみると、はじパタと同じ結果になっていることが確認できました。
まとめ
今回はベイズ分類規則の原理について、Pythonで実装しながらはじパタ3章を読み進めた記録を残しました。
はじパタはきちんと入門のための知識が説明されている反面、一般性を保つために抽象的な記述が多いので理解に苦しむ人が多いはず(かくいう私もそのひとり)。
スムーズに理解するには、なるべく具体的なケースを思い浮かべたり、プログラムを実装しながら読み進めるのがおすすめのやり方です。
この記事に辿り着いた中の誰か一人でも、理解の手助けになれば嬉しいです。
参考
参考URL
1.9. Naive Bayes/scikit-learn公式ドキュメント











コメントを書く