こんにちは、えびかずきです!
今回は勾配法について説明したいと思います。
ここまでの流れを復習したい方は、過去の記事をご覧ください。
https://ebi-works.com/deeplearning-0/
勾配法とは
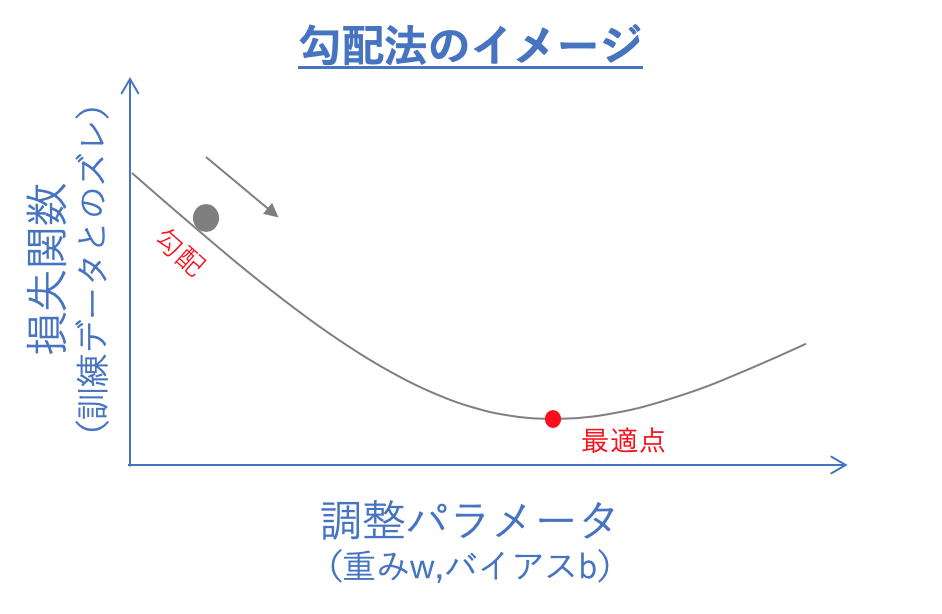
勾配法とは、ニューラルネットワークの重みやバイアス(閾値)の
パラメータを最適値に調整するための学習手法です。
具体的な方法としては、
まずテストデータと訓練データとのズレを表す「損失関数」を定義して、
その値がなるべく小さくなるようにパラメータを調整します。
ちょうど坂を転がるボールのように斜面の勾配に沿って点を移動させて、
勾配がゼロになる最適点まで学習を進めるというイメージです。
開発環境
OS:macOS Catalina ver10.15.2
使用した外部ライブラリ:
numpy1.18.1
matplotlib3.0.3
エディタ:jupyter notebook
ソースコード
github/ebikazuki/deeplearning
本記事では、「#5」のフォルダを使用します。
損失関数
ここでは一般的な損失関数として、
二乗和誤差と交差エントロピー誤差の2例を紹介します。
二乗和誤差
\(E=\dfrac{1}{2}\sum_{k}(y_k-t_k)^2\)
\(y_k\):訓練データの結果ベクトル要素、\(t_k\):訓練データの正解ベクトル要素
二乗和誤差とは、
訓練データの結果(y)と訓練データの正解(t)との差の二乗を
足し合わせるという単純な関数です。
なぜ二乗するかというと、
単純に差を取っただけだとプラスの成分とマイナスの成分が打ち消し合って
ズレの大きさを評価できないからです。(ちょうど統計で分散を計算するのと同じ理由)
係数の1/2の意味は、
後で勾配をとるために微分する時、
綺麗に係数が消えるようするためという実用的な理由です。
勾配法の本質的な理解とは関係がありませんので、
現時点で理解できない場合は深く考えすに読み飛ばしてOKです。
(\(\sum\)の記号は添字のある各要素を足し算するという意味で、シグマと読みます)
それでは、二乗和誤差を実装してみましょう!
#二乗和誤差
import numpy as np
#二乗和誤差(MeanSquareError)関数の定義
#結果データ(y)と訓練データ(t)の差の二乗を足し合わせる
def mean_square_error(y,t):
return 1/2*np.sum((y-t)**2)
#試しにyとtを入れて計算してみる
y=np.array([0,0.1,0,0,0,0.6,0,0,0.2,0.1])
t=np.array([0,0,0,0,0,1,0,0,0,0])
print(mean_square_error(y,t))output :0.11000000000000003
交差エントロピー誤差
\(E=-\sum_{k} t_klog(y_k)\)
\(y_k\):訓練データの結果ベクトル要素、\(t_k\):訓練データの正解ベクトル要素
次は交差エントロピー誤差です。
名前だけ聞くと何やら難しそうな感じかしますが、実は全然難しくありません。
交差エントロピー誤差とは、
one-hot表現の正解データ中で1となっている箇所の訓練データに対して、
対数をとったものです。
といっても意味わかりませんよね(笑)
大丈夫です、ちゃんと説明します。
one-hot表現とは:
例えばone-hot表現で0~9のアラビア数字を表現する場合、「5」は「0,0,0,0,0,1,0,0,0,0,0」という風に表現される。
これを念頭において、交差エントロピー誤差の式をじっくり眺めてみましょう。
one-hot表現で表された訓練データの結果ベクトルt(例えば[0,0,0,1,0,0])は、
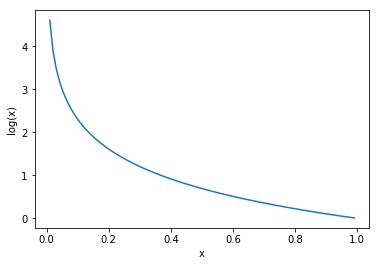
正解の要素だけが1で他は0なので、正解の箇所の\(-log(y_k)\)のみが残ります。
\(-log(y_k)\)nの関数は、下のように1に近づくほど、小さくなってゆくので、
これが正解データとズレと考えることができるのです。
分類問題で出力をone-hot表現にした場合、正解の箇所以外の数値を評価する価値はあまりありませんので、こういった損失関数が適切というわけです。
それでは、交差エントロピー誤差を実装してみましょう。
#交差エントロピー誤差
import numpy as np
#二乗和誤差(CrossEntropyError)関数の定義
#one-hot表現で”1”になっているところのみのズレを評価する誤差関数
def cross_entropy_error(y,t):
delta = 1e-7 #log0は計算できないため、これを回避するための微小値
return -np.sum(t*np.log(y+delta))
#試しにyとtを入れて計算してみる
y=np.array([0,0.1,0,0,0,0.6,0,0,0.2,0.1])
t=np.array([0,0,0,0,0,1,0,0,0,0])
print(cross_entropy_error(y,t))output :0.510825457099338
微分について
微分とは関数のある地点での接線の傾きを求めることです。
※微分なんて知ってるよ、という方は読み飛ばしてOKです。
微分の実装例へ進みましょう。
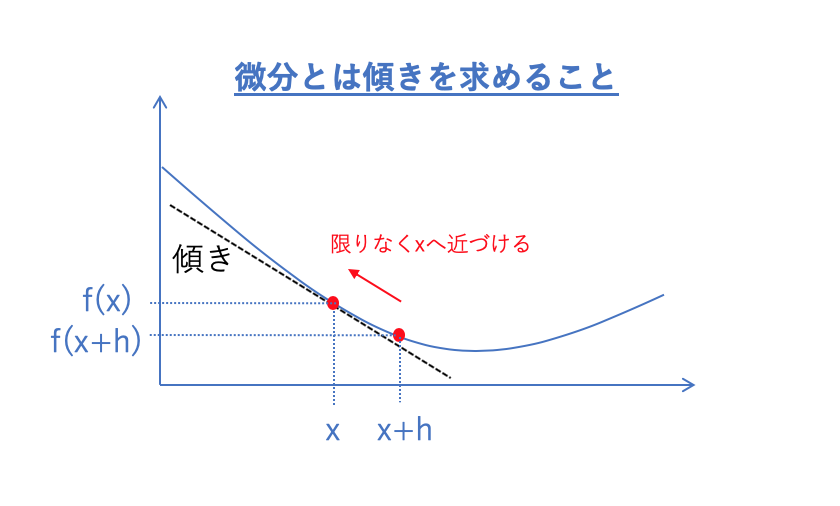
微分のイメージとしては上の図の通りです。
ある地点xとx+hの地点との2点で結ばれた直線の傾きは、\(\dfrac{f(x+h)-f(x)}{h} \)です。
よって、地点xでの接線の傾きを求めるには、
hをだんだん小さくしてx+hを限りなくxに近づけてやれば良いということになります。
したがって微分の定義は以下のようになります。
(ちなみに\(\dfrac{d}{dx}\)は微分を表す演算子です。)
微分の定義:
\(\dfrac{df(x)}{dx}=\lim_{h \to 0}\dfrac{f(x+h)-f(x)}{h} \)
数値演算として実装する場合:
pythonで数値的に実装する場合、定義の式のままで実装するとプラス側の向きの傾きに偏ってしまいます。
そこでバランスを取るためにここでは下の式へ修正します。
\(\dfrac{df(x)}{dx}=\lim_{h \to 0}\dfrac{f(x+h)-f(x-h)}{2h} \)
それでは、数値的な微分演算を実装してみましょう!
#微分を求める関数を定義する
import numpy as np
def numerical_diff(f,x):
h = 1e-4 #微小幅hとして十分小さい数値を入れる
return (f(x+h)-f(x-h))/(2*h)
#試しにf(x)=x**2でdf(5)/dxを計算する
def f(x):
return x**2
numerical_diff(f,5)output :9.999999999976694
偏微分について
偏微分とは、変数が複数ある場合の微分の概念です。
実際その内容はそんなに難しくありません。
注目する変数以外は固定して、注目する変数で微分をするというだけの単純な操作です。
例えば、f(x1,x2)という関数がある場合、
x1でf(x1,x2)を偏微分する場合、\(∂f\∂x1)という風に表記します。
なぜ偏微分が必要かと言うと、
実際にニューラルネットワークで我々が扱う損失関数は上の微分の例のように変数が一つというわけではないからです。
各ノードの重み(w)やバイアス(b)が全て変数となります。
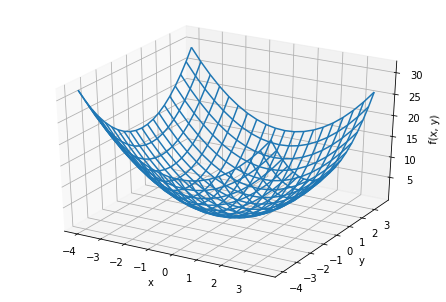
例えば、変数が2つの場合ならば下のような三次元空間のイメージです。
つまり損失関数は変数の数に応じてイメージする空間の次元が増えていきます。(とは言え4次元以上の空間をイメージするのは難しいですが。。。)
勾配法を実装しよう
勾配とは
勾配とは全変数の偏微分のセットのことです。
例えばf(x1,x2)ならば、\(∂f\∂x1,∂f\∂x2)が勾配です。
この勾配を求めることでパラメータを調整する方向が定まり、ニューラルネットワークのパラメータ調整ができるということになります。
では実際に勾配を求めてみましょう!
#勾配(偏微分のセット)を求める関数を定義する
import numpy as np
#勾配関数(xは配列であり複数の次元を持つベクトル)
def numerical_gradient(f,x):
#微小幅hとして十分小さい数値を入れる
h = 1e-4
#grad(勾配)をx配列と同じ形で定義する
grad = np.zeros_like(x)
#xの次元全てにおいて偏微分を求める
for i in range(x.size):
#x[i]を一時保管
tmp = x[i]
#f(x+h)を求める
x[i] = tmp + h
fxh1 = f(x)
#f(x-h)を求める
x[i] = tmp - h
fxh2 = f(x)
#∂f(x_i)/∂x_iを求める
grad[i] = (fxh1 - fxh2) / (2*h)
#x[i]を元に戻す
x[i] = tmp
return grad
#f(x)を定義して勾配関数を試してみる
def f(x):
return np.sum(x**2)
x = np.array([3.0,4.0])
numerical_gradient(f,x)output :array([6., 8.])
勾配降下法
この勾配の各要素の数値が大きいほど正の方向の坂が急になっているということを意味しています。
したがってこの勾配の各要素の数値に応じてパラメータの値を調整してやることによって学習を進められるということになります。
そこで、学習率(learning rate)を導入して、各パラメータ(例えば重みw)を以下のように調整します。
これが勾配降下法です。
\(w_k=w_k-η\dfrac{∂f}{∂w_k}\)
η:学習率,f:損失関数
勾配降下法の実装
さてそれでは勾配降下法を実装してみましょう。
ここでは\(f(x_1,x_2)=x_2^2+x_2^2\)という関数を損失関数に見立てて勾配法を実装します。
#勾配降下法(GradientDescent)
import numpy as np
#勾配降下法の関数を定義する(init_xは初期値、lrは学習率、step_numは学習回数)
def GD(f,init_x,lr=0.1,step_num=100):
x = init_x
#勾配を求める→学習率に応じてxの値を修正 のサイクルを繰り返す
for i in range(step_num):
grad = numerical_gradient(f,x)
x -= lr*grad
return x
#f(x)を定義し初期値xを指定して、勾配降下法を試してみる
def f(x):
return np.sum(x**2)
init_x = np.array([3.0,4.0])
GD(f,init_x,lr=0.1,step_num=100)
output :array([6.11110793e-10, 8.14814391e-10])
ニューラルネットワークへの適用
損失関数の勾配を求める
まずは、手始めにニューラルネットのモデル中で定義した重みパラメータ(W)の勾配を求めるプログラムを実装してみましょう!
#ニューラルネットで損失関数の勾配を求める
import sys, os
sys.path.append(os.pardir) # 親ディレクトリのファイルを参照するため
import numpy as np
from common.functions import softmax
class simpleNet:
def __init__(self):
self.W = np.random.randn(2,3)
def predict(self, x):
return np.dot(x, self.W)
def loss(self, x, t):
z = self.predict(x)
y = softmax(z)
loss = cross_entropy_error(y, t)
return loss
x = np.array([0.6, 0.9])
t = np.array([0, 0, 1])
net = simpleNet()
#numerical_gradient(f,x)を使うためにダミー引数wで関数を再定義
#loss(x,t)のままだと、gradient(loss, net.W)中のloss(net.W)(スクリプト中の表記ではf(x))を実行しようとした時に引数が合っていないので問題が起きる。
#ならば計算に関与しないダミー引数で再定義することで問題を回避するという発想。
f = lambda w: net.loss(x, t)
dW = numerical_gradient(f, net.W)
print(dW)output :
[[ 0.21412288 0.13482767 -0.34895054] [ 0.32118432 0.2022415 -0.52342582]]
ミニバッチ学習について
効率よく学習を進める一つのテクニックとして、
ミニバッチ学習というものがあります。
ミニバッチ学習とは、
沢山の訓練データの中からランダムに少数のバッチを取り出して訓練するという学習方法です。
ディープラーニング学習では、訓練データが数万を超えるような例はザラです。しかしながら一回のパラメータ調整でそれら全てを使うのは多くの処理能力が必要ですし効率があまり良くありません。
ミニバッチでランダムに取り出した少数の訓練データでパラメータ調整を実施し、その後再度ランダムに異なる訓練データを取り出してパラメータ調整を実施するというサイクルを繰り返すことによって効率よく学習が進められるというわけです。
それではミニバッチを生成するプログラムを実装してみましょう!
#mnistデータのミニバッチを生成する
import sys, os
sys.path.append(os.pardir)
import numpy as np
from dataset.mnist import load_mnist
(x_train,t_train),(x_test,t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=True)
#データの形を確認する
print("x_train.shape=",x_train.shape)
print("y_train.shape=",t_train.shape)
train_size = x_train.shape[0] #60000(総数)
batch_size = 10 #バッチサイズを10に指定(任意)
#1~60000からランダムに10個の数字を選ぶ
batch_choice = np.random.choice(train_size,batch_size)
x_batch = x_train[batch_choice]
t_batch = t_train[batch_choice]
print("x_batch=\n",x_batch)
print("t_batch=\n",t_batch)output :
x_train.shape= (60000, 784) y_train.shape= (60000, 10) x_batch= [[0. 0. 0. ... 0. 0. 0.] [0. 0. 0. ... 0. 0. 0.] [0. 0. 0. ... 0. 0. 0.] ... [0. 0. 0. ... 0. 0. 0.] [0. 0. 0. ... 0. 0. 0.] [0. 0. 0. ... 0. 0. 0.]] t_batch= [[0. 0. 0. 0. 0. 0. 1. 0. 0. 0.] [1. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 1. 0. 0.] [0. 0. 0. 0. 0. 0. 1. 0. 0. 0.] [1. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 1. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 1. 0. 0.] [0. 0. 0. 0. 0. 0. 1. 0. 0. 0.] [0. 0. 0. 1. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]]
エポックについて
エポックとは、学習回数の単位です。
エポック=(訓練データ総数/ミニバッチデータ数)回
使ったデータの総数が訓練データの総数と一致するため、学習回数のとしてわかりやすい単位と言えるでしょう。
例えば、10,000個の訓練データを100個のミニバッチで1エポック学習する。と言えば、 100(10,000/100)回の学習をすることになります。
実践編:ニューラルネットワークで勾配降下法を実装する
さあ、いよいよ実践編です。
ニューラルネットで勾配降下法を実装してみましょう!
ここではゼロから作るDeepLearning,斎藤康毅,2016で紹介されているソースコードを使用させていただきます。(スタンフォード大のCS231nという講義で使われているコードを参考にしたそうです。)
記事内にコード埋め込むと長くなりすぎるので、Githubのリポジトリに保存してある「train_neuralnet.ipynb」というファイルをダウンロードして実行してみてください。(コード内で「two_layer_net.py」というスクリプトファイルを使うので、こちらも一緒にダウンロードしてください)
結果
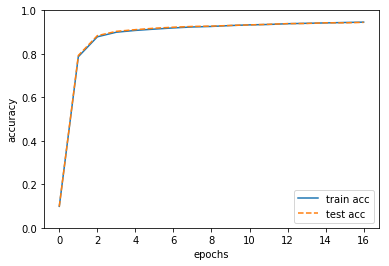
ソースコード実行すると、下のように結果が出力されると思います。
これは横軸にエポック(学習回数)をとって訓練データ、テストデータそれぞれの精度(train acc,test acc)の向上具合を示したものになります。
ここでは特にテストデータの精度(test acc)が重要です。なぜなら訓練に使ってないデータでも精度の良い結果を出せていると判断できるからです。
16エポック学習して、精度は1.0にかなり近いところまで向上していることがわかります。
まとめ
今回は、ニューラルネットワークのパーラメータ調整を実施するための手法として、勾配法について説明しました。
今回までの記事で、ひと通りニューラルネットワークの基礎的な理論については説明し尽くしました。
あとは層を深くしたディープラーニングで如何に精度良く、実用的なモデルを実装するかという話に入っていきます。
なんだかワクワクしてきますね!
次回は、「第6回:誤差逆伝播法を実装しよう!」です。
乞うご期待!
参考書籍
今回記事内で使用したソースコードは「ゼロから作るDeeplearning」のものを改変して使用させていただきました。












コメントを書く