こんにちは、えびかずきです!
今回はニューラルネットワークのモデルを実装する方法について説明していきます。
ここまでの流れを復習したい方は、過去の記事をご覧ください。
https://ebi-works.com/deeplearning-0/
ニューラルネットワークの実装
では早速ニューラルネットワークを作っていきましょう!
ネットワークモデル
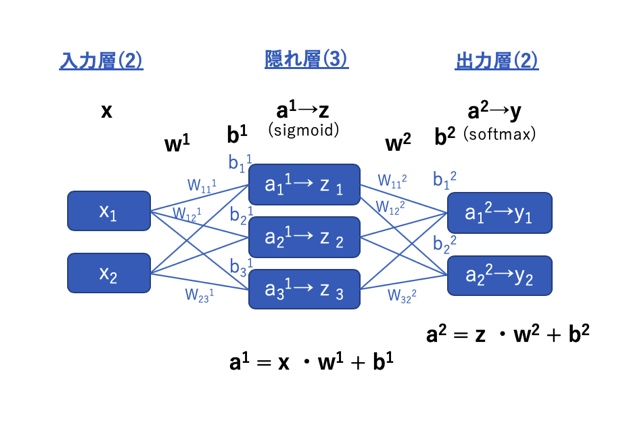
まずは今回作るニューラルネットワークのモデルを決める必要があります。
この記事ではニューラルネットワークを学ぶということを目的としていますので、理解を助けるために極力単純なモデルで試してみることにします。
下図のように、
入力層(データ数:2)→隠れ層(データ数:3)→出力層(データ数:2)
からなる3層構造のニューラルネットワークを作ることにします。
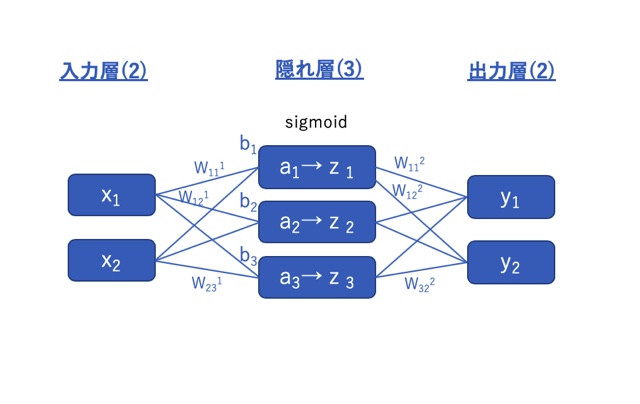
w:重み、b:閾値(符号反転;和の演算をするため)
補足:何層重ねたらディープラーニング?
上の簡単なモデルからさらに隠れ層を2層、3層、4層と増やして層を深くしていくことで「ディープラーニング」と呼ばれるようになります。何層からディープラーニングかは曖昧な部分がありますが、隠れ層を複数持つニューラルネットワーク構造における呼称だと筆者は認識しています。
ちなみに画像分類で有名なVGG19などでは19層もの層を重ねたニューラルネットワークでディープラーニングを実装しています。
開発環境
OS:macOS Catalina ver10.15.2
使用した外部ライブラリ:
numpy1.18.1
matplotlib3.0.3
pillow7.0.0
ここでは新しくpillowというライブラリを使います。
下のようにしてpipでインストールできます。
$ pip install pillowエディタ:jupyter notebook
ソースコード
github/ebikazuki/deeplearning
本記事では、「#4」と「dataset」と「common」のフォルダを使用します。
ニューラルネット ワークの試作
下のサンプルがニューラルネットワークを実装するコードになります。
作り方を説明をしてからコードを組むという流れだと、前置きがとても長くなりそうだったので、まずは出来上がりを見て全体を俯瞰してみてください。
内容は、上で紹介した3層ニューラルネットワークを作り、入力xに1,2を入れて計算を実行するというコードになっています。
#ニューラルネットワークの試作-1
import numpy as np
#活性化関数の定義
def sigmoid(x):
return 1 / (1 + np.exp(-x))
#入力層(1層目)
x = np.array([1,2])
#隠れ層(2層目)
w1 = np.array([[0.1,0.3,0.5],[0.1,0.3,0.5]])
b1 = np.array([0,-0.8,-0.5])
a1 = np.dot(x,w1) + b1
z = sigmoid(a1)
#出力層(3層目)
w2 = np.array([[0.5,1],[0.5,1],[0.5,1]])
b2 = np.array([0,0])
y = np.dot(z,w2) + b2
print('x=\n',x)
print('y=\n',y)結果として、出力yとして0.915…,1.830…が出てきました。
x= [1 2] y= [0.91524014 1.83048028]
意外とコードは短いと感じませんでしたか?
この段階では中身は理解できなくても、割とスッキリしてるなということだけわかってもらえればOKです。
それでは1つずつ説明していきます!
行列の積
上のコードが意外とスッキリしていた理由は、「行列の積」を使って計算を一気にまとめて処理しているためです。
これは高校数学の数Cで学ぶ内容ですが、ここで使う内容だけなら正直簡単なのでざっと説明していきます!
既に知ってるよ!という方は「ニューラルネットワークのコード説明」まで飛ばしてOKです。
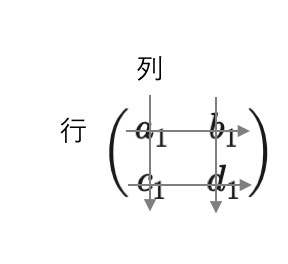
行列とは
行列とは、文字の如く行と列からなる数値の集まりのことです。(下図参照)
縦が列、横が行です。ちょうどエクセルのシートのようなものをイメージすると分かりやすいと思います。
下図の例は、2×2(行×列)行列です。
こういった数のまとまりを1セットにして行列とすることで、ニューラルネットワークの計算を簡単にすることができます。
こういった考え方を導入しないと、ネットワークが大きくなればなるほどパーセプトロンの時のような重み付きの足し算が膨れ上がってしまいます。
そんなことになってはコードとして記述するのは大変になってしまいますからね。
行列で計算をまとめる
行列を使ったニューラルネットワークの計算は、下図のようなイメージです。
入力x、重みw、閾値(符号反転)b、重み付き和a、隠れ層出力z、出力yを各層でひとまとめにした行列として取り扱います。
そうすることで図中下部に示すように計算はスッキリします。
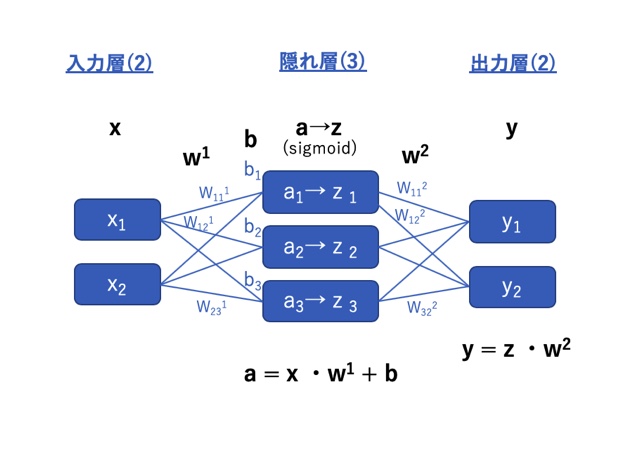
行列の形について:
この例だと重みw以外は全て1行または1列のベクトル( 1×N or N×1行列)なのでなんだか行列っぽくない感じがしますが、下の行列の積を適用して演算できるのでご安心を。
行列の積
では行列の積について説明します。
積は以下のように定義されています。
\[ \left( \begin{array}{ccc} a_1 & b_1 \\ c_1&d_1 \end{array} \right) \left( \begin{array}{ccc} a_2 & b_2 \\ c_2&d_2 \end{array} \right) =\left( \begin{array}{ccc} a_1a_2+b_1c_2 & a_1b_2+b_1d_2 \\ c_1a_2+d_1c_2&c_1b_2+d_1d_2 \end{array} \right) \]
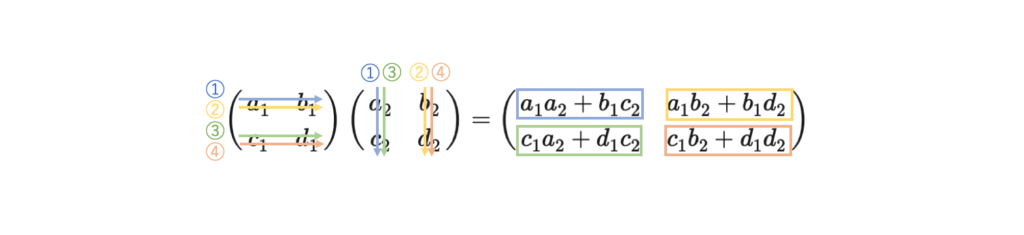
図の通り番号同士の行と列を掛けて足していきます。
具体的には、
①まず左行列の第1行と右行列の第1列のそれぞれの要素を掛けて足したものを、結果の行列の1行目の1列目に配置します。
②次に左行列の第1行と右行列の第2列のそれぞれの要素を掛けて足したものを、結果の行列の1行目の2列目に配置します。
③次に左行列の第2行と右行列の第1列のそれぞれの要素を掛けて足したものを、結果の行列の2行目の1列目に配置します。
④次に左行列の第2行と右行列の第2列のそれぞれの要素を掛けて足したものを、結果の行列の2行目の2列目に配置します。
ちなみに行列の積では交換法則が成り立ちません。つまり積の左右を逆転させると結果が変わります(AB≠BA)ので気をつけてください。
PythonではNumPyライブラリのドット積メソッド(dot)で行列(NumPy配列)の積が計算できるようになっていますのでx、w、a、b、yなどの行列を作って計算するということです。
行列の積はやり方さえ覚えてしまえば単純です。最初は混乱してしまうと思いますが、下の計算例を参考に頭に定着させてください。
計算例1
2×2行列同士の積をPythonで計算してみましょう。
\[ a= \left( \begin{array}{ccc} 0 & 1 \\ 2&3 \end{array} \right),b= \left( \begin{array}{ccc} 1& 2 \\ 3&4 \end{array} \right) \]
\[ c= \left( \begin{array}{ccc} 0 & 1 \\ 2&3 \end{array} \right)\left( \begin{array}{ccc} 1& 2 \\ 3&4 \end{array} \right) = \left( \begin{array}{ccc} 3 & 4 \\ 11&16 \end{array} \right) \]
#行列の掛け算-1
import numpy as np
a = np.array([[0,1],[2,3]])
b = np.array([[1,2],[3,4]])
c = np.dot(a,b)
print('a=\n',a)
print('b=\n',b)
print('c=\n',c)出力:
a= [[0 1] [2 3]] b= [[1 2] [3 4]] c= [[ 3 4] [11 16]]
計算例2
次は、1×4行列と4×2行列の積を計算してみましょう。
行列の形は同じでなくてもOK。
左行列の列と右行列の行が一致していれば計算可能です。
\[ a= \left( \begin{array}{ccc} 1 & 2&3&4 \end{array} \right),b= \left( \begin{array}{ccc} 1& 2 \\ 3&4\\5& 6 \\ 7&8 \end{array} \right) \]
\[ c= \left( \begin{array}{ccc} 1 & 2&3&4 \end{array} \right)\left( \begin{array}{ccc} 1& 2 \\ 3&4\\5& 6 \\ 7&8 \end{array} \right) = \left( \begin{array}{ccc} 50 & 60 \end{array} \right) \]
#行列の掛け算-2
import numpy as np
a = np.array([1,2,3,4])
b = np.array([[1,2],[3,4],[5,6],[7,8]])
c = np.dot(a,b)
print('a=\n',a)
print('b=\n',b)
print('c=\n',c)出力:
a= [1 2 3 4] b= [[1 2] [3 4] [5 6] [7 8]] c= [50 60]
エラー例(左の列数と右の行数が合っていないと計算できない)
行列の積はどんな行列同士でもできると言うわけではありません。
下の例のように左の列数と右の行数が一致していない場合は計算できません。
Pythonで計算を実行すると下のようにエラーを吐き出します。
\[ a= \left( \begin{array}{ccc} 0 & 1&2&3 \end{array} \right),b= \left( \begin{array}{ccc} 0&1& 2&3\\ 1& 2&3&4 \end{array} \right) \]
\[ c= \left( \begin{array}{ccc} 0 & 1&2&3 \end{array} \right)\left( \begin{array}{ccc} 0&1& 2&3\\ 1& 2&3&4 \end{array} \right) = 計算できない \]
#行列の掛け算-エラー例
import numpy as np
a = np.array([0,1,2,3])
b = np.array([[1,2,3,4],[1,2,3,4]])
c = np.dot(a,b)出力:
--------------------------------------------------------------------------- ValueError Traceback (most recent call last) <ipython-input-14-a98cb7ef74d6> in <module> 5 a = np.array([0,1,2,3]) 6 b = np.array([[1,2,3,4],[1,2,3,4]]) ----> 7 c = np.dot(a,b) 8 9 print('a=\n',a) <__array_function__ internals> in dot(*args, **kwargs) ValueError: shapes (4,) and (2,4) not aligned: 4 (dim 0) != 2 (dim 0)
ニューラルネットワークのコード説明
ニューラルネットワークではいかに重み付きの和をまとめて計算できるかということが重要になってきます。
ちょうど計算例2のように(N行×1行)と(M行×N行)の計算を繰り返しています。
行列の積を理解した今なら、ニューラルネットワークのコードが理解できるようになっていると思いますので、じっくり中身を見てみましょう。
※説明はコード内に記載しました。
#行列演算の部分だけ抜き出したもの
#入力層として配列xを定義する(1層目)
x = np.array([1,2])
#重みw1,バイアスb1を定義する(2層目)
w1 = np.array([[0.1,0.3,0.5],[0.1,0.3,0.5]])
b1 = np.array([0,-0.8,-0.5])
#行列の積を使って、x,w1,b1からa1を計算する(2層目)
#np.dot()が行列の積を行うメソッド
a1 = np.dot(x,w1) + b1
#a1をsigmoid関数に入れてzを出力する(2層目)
z = sigmoid(a1)
#出力層(3層目)
#2層目と同様に重みw2とバイアスb2を定義し、行列の積を使ってyを出力する
w2 = np.array([[0.5,1],[0.5,1],[0.5,1]])
b2 = np.array([0,0])
y = np.dot(z,w2) + b2ニューラルネットワークの改良
もう山は超えました。
後は実用的なことを考えてちょっとずつ改良を加えていきます。
ニューラルネットワークで分類問題を解こうとする場合、上で作ったニューラルネットワークだと得られる出力の意味がわかりにくいと言う問題があります。
そこで出力層にも活性化関数を導入して出力を分類の確率という形に変換することを考えます。
出力層の活性化関数
ソフトマックス関数
分類の確率を出力するためには、ソフトマックス関数をつかいます。
ソフトマックス関数とは、以下に示す関数です。
\(y_k=\dfrac{e^{a_k}}{\sum_{i=0}^n e^{a_i}}\)
これは出力の各要素全体の確率を1とした場合、k番目が正解である確率(※1)を表しています。
ニューラルネットワークの試作で作ったコードでは出力yとして0.915…,1.830…が出てきましたが、こういった結果よりは、全体を1として、それぞれの確率に変換されている方が結果を解釈しやすいですからね。
※1ソフトマックス関数の値がなぜ確率になるか?
これはソフトマックス関数で得た数値が確率として解釈可能というだけであって、統計学的な確率(ある事象/全事象)とは異なる点に注意が必要です。
出力層までたどり着いたaの値のそれぞれの大小関係を保ちつつ全体を1として正規化し確率的な解釈を与えたいという目的を達成するために、指数関数を使うのが妥当というだけです。
加えて、第6回で説明する「誤差逆伝播法」使いやすい関数形をわざと設計しているという実用面の工夫も実は含まれています。
恒等関数
分類問題でなく出力の調整が必要なければ、出力層に活性化関数を導入する必要はありません。
しかしながら、ソフトウェアとしてニューラルネットワークを形式的に定義して、明示的に出力層の活性化関数を導入したい場合には、
恒等関数として何も変わらない関数を実装する場合もあります。
改良ニューラルネットワークの実装
それでは、出力層にソフトマックス関数を導入して、ニューラルネットワークの改良版を作ってみましょう!
#ニューラルネットワークの試作-2(出力層の改良)
import numpy as np
#softmax関数の定義
def softmax(a):
exp_a = np.exp(a)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
#活性化関数の定義
def sigmoid(x):
return 1 / (1 + np.exp(-x))
#入力層(1層目)
x = np.array([1,2])
#隠れ層(2層目)
w1 = np.array([[0.1,0.3,0.5],[0.1,0.3,0.5]])
b1 = np.array([0,-0.8,-0.5])
a1 = np.dot(x,w1) + b1
z = sigmoid(a1)
#出力層(3層目)
w2 = np.array([[0.5,1],[0.5,1],[0.5,1]])
b2 = np.array([0,0])
a2 = np.dot(z,w2) + b2
#最後にa2をsoftmax関数で処理して、yを出力とする(ここが重要!)
y = softmax(a2)
print('x=\n',x)
print('y=\n',y)出力:
x= [1 2] y= [0.28592874 0.71407126]
それぞれの確率が出力されましたね。足したら1になるのも確認できました。
オーバーフローを防ぐために
ソフトマックス関数は指数関数なので、代入するaの値が大きいとオーバーフロー(コンピュータが処理できる数値を超える)が発生してしまいます。
そのため、下のようにオーバーフローが起きにくくする工夫を加えるのが一般的です。
aの中で最も大きいものを抽出してcという変数を定義して、それとの差分を使って処理をするという方法です。
これなら結果は変えずに、計算途中で爆発的に大きい数の発生を防ぐことができます。
今後はソフトマックス関数を使う場合はこちらを使っていきます。
#softmax関数の改良(オーバーフローを回避するsoftmax関数)
def softmax(a):
c = np.max(a)
exp_a = np.exp(a - c) #差分をとって計算する
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y実践編:OCRの実装
最後に、実践編としてOCRの実装をしてみましょう!
OCR(Optical Character Recognition)とは光学的文字認識のことで、要するに手書きなどの文字を読み取るという事です。
ここではゼロから作るDeepLearning,斎藤康毅,2016で紹介されているプログラムを活用させていただきたいと思います。
MNISTとは
手書き文字のサンプルとしては、機械学習の世界で有名なMNISTというデータベースのサンプルを使用します。
http://yann.lecun.com/exdb/mnist/
ここには0〜9の数字について、7万もの手書き文字(下図参照)とそのラベルが蓄積されており、機械学習の研究分野でよく使われます。

MNIST画像の取り込み
では実際に実装してみましょう。
※ここではMNISTデータのダウンロードなどサポートのプログラムとして「dataset」というローカルフォルダを使用します。
ソースコードの欄に示したgithubからダウンロードしてお使いください。
#mnistの手書き画像を確認する
import sys, os
#親ディレクトリのパスを追加(datasetのフォルダにアクセスするため)
sys.path.append(os.pardir)
import numpy as np
from dataset.mnist import load_mnist
from PIL import Image
#mnistデータをダウンロードする
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=False, flatten=True, one_hot_label=False)
#mnist訓練データの画像(0番目)を選択
img = x_train[0]
#1次元で画像データをダウンロードしているのでリシェイプする
img = img.reshape(28, 28)
#fromarrayで配列を画像化できる
img = Image.fromarray(img)
img.show()このコードを実行すると、MNISTの手書き文字データベース(60MB程度)がダウンロードされて、その証拠として下のように手書き画像が表示されます。
最初に実行する時はデータのダウンロードのために少々時間がかかりますが、
一度実行すると、pkl形式(※2)でデータベースのオブジェクトがローカル(databaseフォルダ内)に保存されますので、2回目以降はすぐに使えます。
(※2)pkl形式とは:
Pythonにはpickleという標準ライブラリがあり、プログラムとして実行したオブジェクトをPC上に保存しておくという機能があります。
上のコードではそんなコードは見当たらないですが、実はサポートとして使った「load_mnist」という関数の中にpklで保存するというプロブラムが内蔵されています。
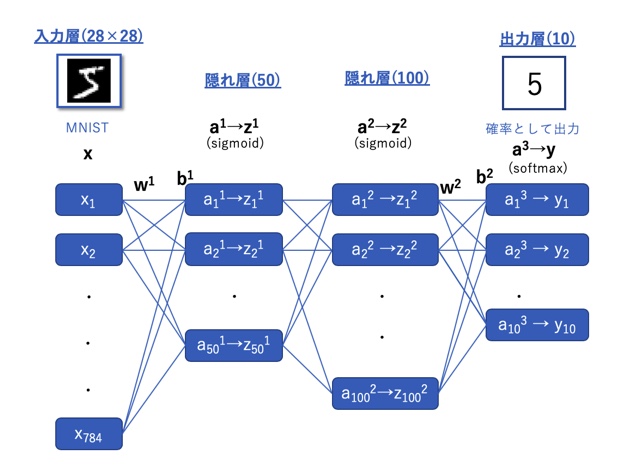
OCRニューラルネットワークのモデル
今回は下のような、モデルでOCRを実装していきます。
OCRの実装
OCRを実装するコードが以下になります。
コードの説明はコメントアウトとしてコード中に記載しましたので参考にしてください。
import sys, os
sys.path.append(os.pardir)
import numpy as np
import pickle
from dataset.mnist import load_mnist
from common.functions import sigmoid, softmax
#mnistのデータを取得する関数を定義
#load_mnistの引数はそれぞれ、
#normalize:色の濃さを数値を0~1に規格化するか
#flatten:各手書き画像のデータを1次元の配列にするか
#one_hot_label:ラベルを0~9の数値ではなく,[0,1,0,0,0,0,0,0,0,0]のようなone-hotにするか
def get_data():
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
return x_test, t_test
#ニューラルネットワークに入力データを入れて計算する関数を定義
def predict(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = softmax(a3)
return y
#実際にOCRの計算を実行する
#x(テストデータ),t(正解ラベル)にMNISTのデータを入れる
x, t = get_data()
#networkに既にパラメータが調整されたニューラルネットワークを入れる(ローカルフォルダから取得)
network = pickle.load(open("sample_weight.pkl",'rb'))
#for文でひとつずつ計算する
#結果が正解ラベルと一致したらaccuracy_cntを足していき正答率をカウントする
accuracy_cnt = 0
for i in range(len(x)):
y = predict(network, x[i])
p= np.argmax(y) # 最も確率の高い要素のインデックスを取得
if p == t[i]:
accuracy_cnt += 1
#正答率(Accuracy)を出力
print("Accuracy:" + str(float(accuracy_cnt) / len(x)))出力:
Accuracy:0.9352
結果として、正答率93.52%という、精度の高いOCR作ることができました!(とはいっても今回はパラメータ調整済みのネットワークを使ったからですが)
バッチ処理の実装
最後に、バッチ処理という概念を説明しておこうと思います。
ニューラルネットワークでは行列の積を使ってまとめて処理をするということを説明しましたが、
さらに範囲を広げて、複数のテストデータや訓練データをまとめて処理するというところまで拡張することができます。
これがバッチ処理の考え方です。
以下のコードでは、OCRのニューラルネットワークで10000個のテストデータを100個ずつのバッチに分けて、それぞれ一気に計算しています。
具体的な内容としては単純で、入力の行列が1×N行列だったのが、M×N行列になるだけです。(例えばOCRの例の場合、N=784(ピクセル数),M=100(バッチ数))
このように処理した方が、計算が早く終わることがあります。
x, t = get_data()
network = pickle.load(open("sample_weight.pkl", 'rb'))
batch_size = 100 # バッチの数
accuracy_cnt = 0
for i in range(0, len(x), batch_size):
x_batch = x[i:i+batch_size]
y_batch = predict(network, x_batch)
p = np.argmax(y_batch, axis=1)
accuracy_cnt += np.sum(p == t[i:i+batch_size])
print("Accuracy:" + str(float(accuracy_cnt) / len(x)))まとめ
今回はニューラルネットワークの作り方について説明しました。(思ったより記事が長くなってしまいました。。。)
行列を知らない人にとっては少し難しかったかもしれませんが、内容を知ってしまうと意外と単純だと思いませんでしたか?
もしご質問あれば下部の問い合わせ欄から入力いただければ、なるべく対応するようにしたいと思います。
さて次回は、以下に重みを調整して学習を進めるかという内容に入っていきます。
次は「#5 勾配法を実装しよう!」です。
乞うご期待!
参考書籍
今回記事内で使用したソースコードは「ゼロから作るDeeplearning」のものを改変して使用させていただきました。










コメントを書く