活性化関数を作ろう！【作って理解するディープラーニング#3】

こんにちは、えびかずきです！

前回はディープラーニングの基礎となるパーセプトロンについて学びました。
しかし当然ながらそれだけではディープラーニングは出来ません。

なぜなら、どうやって学習（重みを最適化）するか？
という問題が未解決だからです。

今回はその足がかりとなる活性化関数について説明していきます。

ここまでの流れを復習したい方は、過去の記事をご覧ください。
https://ebi-works.com/deeplearning-0/

1. 活性化関数とは
- 1.1. なぜ活性化関数について考えるのか？
- 1.2. パーセプトロンとニューラルネットワークの違い
2. 活性化関数を実装しよう
3. まとめ
4. 参考書籍

活性化関数とは

活性化関数とは、入力を出力に変えるための関数です。

実際に脳の中にあるニューロンでは一定量の入力が蓄積されるとシナプスから伝達物質が放出されて出力になるとされていますが、その情報の受け渡しを表現する関数が、すなわち活性化関数です。

なぜ活性化関数について考えるのか？

前回の「パーセプトロンを作ろう」で勉強したステップ関数（閾値を設定する方法）も活性化関数の一例ですが、ディープラーニングに使うためにはある問題点があります。

それは解を最適化する学習の仕組みを導入しづらいということです。

ディープラーニングで解を最適化する方法を大雑把に説明すると、ちょっとずつ重みを調整して出力が目的に合うように調整するというやり方です。

でもステップ関数は見るからにカクカク（※１）していて少し重みを調整しても出力に変化は生じません。でもある地点まで来るといきなり出力が変わる（０→１or１→０）ということになってしまいます。

これだとまずいので、重みを調整しやすい他の滑らかな活性化関数を考える必要があるのです。

今回の記事ではステップ関数に加えて、
ディープラーニングでよく使うシグモイド関数とReLU関数を紹介します。

さらに詳しく※１
カクカクしていて不連続なポイントでは微分ができません。
すなわち変化量が見積もれないので調整が困難になります。

パーセプトロンとニューラルネットワークの違い

いろいろ専門用語が出てきて頭の整理が難しいですが、ここで少し言葉の定義について考えておこうと思います。

結局パーセプトロンとニューラルネットワークって何が違うの？という疑問が浮かんできますが、私は正直それぞれの明確な定義を説明している記事や書籍は見たことがありません。

私の解釈では、
パーセプトロンはニューラルネットワークの一部という風に考えています。

パーセプトロン：
ニューロンの仕組み（McCulloch-Pittsモデル）を模倣した情報認識アルゴリズム。活性関数は主にステップ関数。多層パーセプトロンではシグモイド関数を使うこともある。

ニューラルネットワーク：
ニューロンによる脳内のネットワーク構造を模倣した数理モデル。
パーセプトロンよりも広義。

ニューラルネットワークでは、CNN(畳み込みニューラルネット：画像認識に使う)RNN(リカレントニューラルネット：時系列データ認識に使う)などの発展的な内容も含まれ、ニューロンの仕組みに拘らず機械学習の性能に目を向けた実用的な印象があります。

活性化関数を実装しよう

開発環境

OS:macOS Catalina ver10.15.2

使用した外部ライブラリ:
numpy1.18.1
matplotlib3.0.3

エディタ：jupyter notebook

ソースコード

github/ebikazuki/deeplearning
本記事では、deeplearning#3.ipynbを使用します。

ステップ関数

%matplotlib inline

#必要なライブラリをインポート
import numpy as np
import matplotlib.pylab as plt

#ステップ関数を定義
def step(x):
    x = x > 0
    return x.astype(np.int)

#グラフを表示
X = np.arange(-10, 10, 0.1)
Y = step(X)
plt.plot(X, Y)
plt.ylim(-0.1, 1.1)
plt.show()

ステップ関数は前回のパーセプトロンの説明でも実装しましたが、今回は今後のことを考えて引数としてNumPy配列を受け取れるように改良してあります。

内容を説明すると、まず関数中の不等号

x > 0

は、xの値の応じてTRUEまたはFALSEのブーリアンになります。
（例えばxが1ならTRUE、-1ならFALSEです。）

xは配列であってもよく、その場合各要素で不等号の判定が行われます。

さらに、

x.astype(np.int)

は「xを整数型に変換せよ」という命令になります。

元の型がブーリアンの場合は、TRUE→1,FALSE→0と変換されます。

ということで、パッと見では中身を理解しづらいですが、上記のコードはxが0を超えると1、xが0以下なら0を出力するステップ関数となるのです。

シグモイド関数

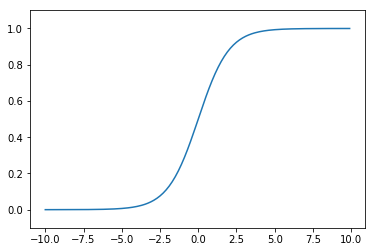
シグモイド関数とは、

\(f(x)=\dfrac{1}{1+\mathrm{e}^{-x}}\)

のような表される関数です。

実装すると以下のようなコードになります。

%matplotlib inline

#必要なライブラリをインポート
import numpy as np
import matplotlib.pylab as plt

#シグモイド関数を定義
def sigmoid(x):
    return 1 / (1 + np.exp(-x))    

#グラフを表示
X = np.arange(-10, 10, 0.1)
Y = sigmoid(X)
plt.plot(X, Y)
plt.ylim(-0.1, 1.1)
plt.show()

ステップ関数と比べると、変化が滑らかになっています。

この滑らかさが今後ニューラルネットの重み調整で重要になってきます。

ReLU関数

活性化関数としてもう一つ紹介しておきたいのがReLU（Rectified Linear Unit）関数です。ランプ関数とも呼ばれることがあります。

単純ながら非線型性を保ちつつ斜面の調整しろを用意していて、学習による重み調整がしやすい仕様になっています。

%matplotlib inline

#必要なライブラリをインポート
import numpy as np
import matplotlib.pylab as plt

#ReLU関数を定義
def relu(x):
    return np.maximum(0, x)

#グラフを表示
x = np.arange(-10, 10, 0.1)
y = relu(x)
plt.plot(x, y)
plt.ylim(-1.0, 10.5)
plt.show()

ReLU関数は、

maximum(0,x)

で実装されます。

これは「0かxの大きい方を取れ」という命令になっています。