こんにちはえびかずきです!
今回は「偏差値とは何か?についてPythonで実装しながら説明したいと思います。
開発環境
OS:macOS Catalina ver10.15.2
使用した外部ライブラリ:
・numpy1.18.1
・matplotlib3.0.3
・csv
エディタ:jupyter notebook
偏差値を計算する数式
まず、偏差値とは、以下に示す数式で表されます。
偏差値=\(50+10×\dfrac{x-μ}{σ}\)
x:テストデータ,μ:平均値,σ:標準偏差
これをPythonで関数として記述して実装していきます。
偏差値の算出には、μ(平均値)とσ(標準偏差)が必要になります。
μ(平均値)はわかると思いますが、σ(標準偏差)は、以下の通りです、
\(σ=\sqrt{\dfrac{\sum_i{(x_i-μ)^2}}{n}}\)
\(x_i\):母集団データ,n:データ数,μ:平均値
標準偏差はデータのばらつき度合いを表します。
標準偏差の計算を関数として実装する
実装例
では実際に実装していきましょう!
偏差値を計算する関数としてdev_value(test,data)実装した例を貼り付けました。
引数は以下のとおりです。
・test:テストデータ(整数 or 浮動少数点)
・data:母集団のリストデータ(1次元のリスト)
#偏差値関数
#dev_value(test,data)
import numpy as np
import csv
def dev_value(test,data):
'''
<引数の説明>
test:テストデータ(int or float)
data:母集団のデータ(一次元list)
'''
#detaを処理しやすいようにnumpy配列に変換する
data = np.array(data)
#sum:合計値/n:データ数/ave:平均値/std:標準偏差を計算
sum = np.sum(data)
n = len(data)
ave = sum/n
std = np.sqrt(np.sum((data - ave)**2)/n)
#最後に偏差値を計算してreturnとする
return 50 + (test - ave)/std*10
if __name__ == '__main__':
"""
<メイン実行コード>
引数のtest,dataを入力することで、結果を出力する。
・母集団csvのアドレスを入力>>>csv形式ファイルアドレス
・数値を入力>>>テストデータを手入力
"""
#母集団データの読み込み
data = []
with open(input("母集団csvのアドレスを入力>>>")) as f:
for row in csv.reader(f):
data.append(int(row[0]))
#テストデータの読み込み
test = int(input("数値を入力>>>"))
#計算結果の出力
print("偏差値=",dev_value(test,data))
コードの説明
下準備として引数の母集団データからsum(総数), ave(μ:平均値),std(σ:標準偏差)を計算し、
最後に偏差値を計算するという流れとしています。
細かい説明はコード中に記載しました。
以下のコードはこのスクリプトが、呼び出しでなくメインで実行された場合に実行されるコードです。
if __name__ == '__main__':ここでは、
引数を要求して、データを提供することで偏差値が計算されるようにしました。母集団データはcsv形式のファイルを想定しています。
下のような形式のcsvを取り込めるようにしていますので、
遊べるようにサンプルファイルを貼り付けておきます。
(実装したスクリプトと同じディレクトリに置いて使用ください。)
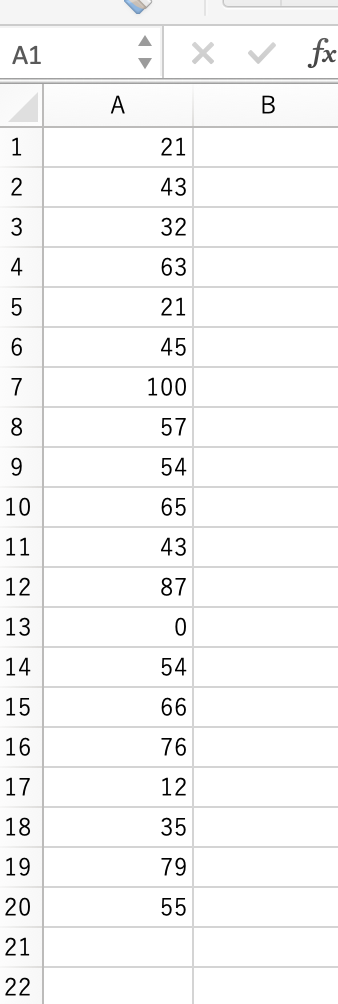
たとえば、以下のように入力した場合、
入力:
母集団csvのアドレスを入力>>>test.csv
数値を入力>>>90
下の出力を得ることができました。
出力:
偏差値=53.84974448670179
結局偏差値とは何なの?
結局のところ偏差値とは、計算式からわかるように、
統計学的に平均からどのくらい離れているかを示した値です。
偏差値:
x=平均値+σの場合:60
x=平均値の場合 :50
x=平均値-σの場合:40
といった具合に平均値の場合を50として、σ離れるごとに10ポイント数値が変化します。
ただこれだけでは統計に慣れている方でないとイマイチその意味が掴みにくいと思います。
数値がσ離れるということが何を意味しているのか?
その答えは正規分布とσの関係をイメージすると理解しやすいです。
正規分布は下の数式であらわされる関数です。
\(f(x)=\dfrac{1}{\sqrt{2πσ}}\exp{-\dfrac{(x-μ)^2}{2σ^2}}\)
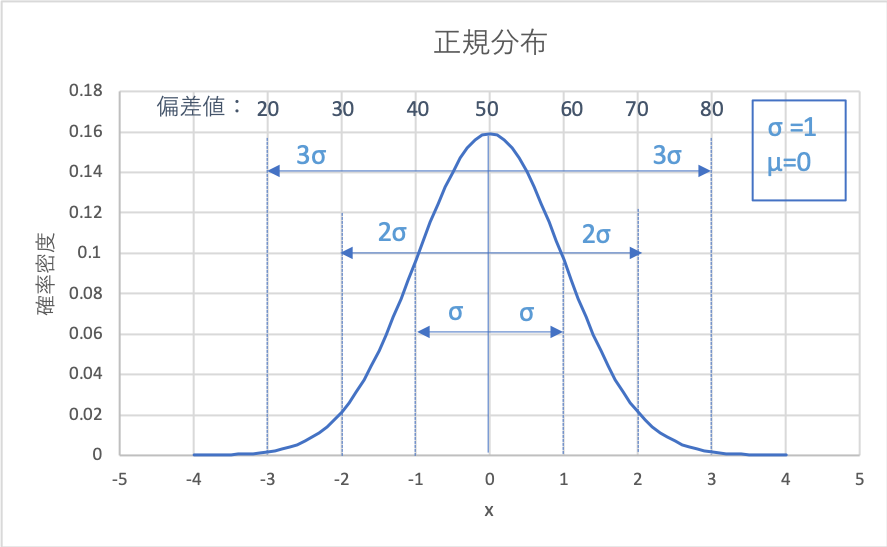
xが各範囲に入る確率はそれぞれ、
xが各範囲に入る確率:
x=μ-σ〜μ+σ(偏差値40〜60):68.27%
x=μ-σ〜μ+σ(偏差値30〜70):95.45%
x=μ-σ〜μ+σ(偏差値20〜80):99.73%
といった値になります。
つまり正規分布に従う母集団の中で、偏差値が例えば70ならば、
成績は上位5%以内くらいのとても良い結果だという風に捉えることができるのです!
偏差値計算であつかうようなデータの集団の多くは正規分布に従うバラツキで分布しています。
歴史的には19世紀の数学者ガウスが天体測量の精度解析で、
データのばらつきが正規分布に従うことを発見したところから来ているようですが、
人間の身長、体重などもその例で、学校のテストの成績も多くの場合正規分布をとります。
しかし場合によっては正規分布に従わず二極化した分布をとったりすることもありますので、
母集団の分布がどうなっているのかを確認することがとても大事です。
ちなみに上の実装例で試したtest.csvの母集団データは、わざと正規分布に近い形にしています。
以下のコードでヒストグラムを確認できます。
#test.csvを読み込んだdataのヒストグラム
%matplotlib inline
import matplotlib.pyplot as plt
plt.title('histogram')
plt.ylabel('freq.')
plt.hist(data)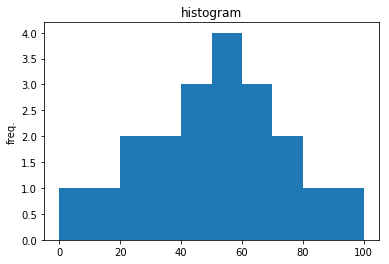
正規分布に従わない例
正規分布に従わない身近な例として、年収があります。
年収は多数の低所得者と少数のお金持ちという左右非対称な分布と取っています。(これが平均年収はあてにならないという理由です。)
まとめ
今回はPythonで偏差値を計算する方法と、偏差値の意味について説明しました。
受験を経験した方の多くは、偏差値を気にしていたと思いますが、
その意味をきちんと理解できていたでしょうか?
これを機にその意味をもう一度確認しておきましょう。
学校の先生や塾の先生など、偏差値を計算する需要のある方はぜひご活用ください!
まあ普通はエクセルでやるでしょうけど。。。笑
参考書籍
執筆にあたり、下記の書籍を参考にさせていただきました。











コメントを書く