Pythonで代数計算する方法
今回はPythonで微分や積分などの代数計算をする方法、そしてそれをグラフ化する方法について説明したいと思います。
開発環境
- 使用言語:Python3
- 使用ライブラリ:sympy
- IDE:jupyter notebook
基本的には代数処理向けライブラリである”sympy”を使って計算をします。
※もしインストールしていない方は、pipなどでインストールしておいてください。
代数処理の基礎
以下のコードがSympyで代数処理を行うための基礎的な手順になります。
取り扱う変数(ここではx)をシンボルオブジェクトとして定義してから代数処理を行います。
シンボルオブジェクトへの数値代入には、.subsメソッドを使います。
#sympyライブラリの全てのオブジェクトをインポート
from sympy import *
#シンボルオブジェクトxを定義
x = Symbol('x')
#yをxの関数として定義
y = x**2
#yの変数xへ2を代入
y.subs({x:2})>> 4xに2を代入することで、
\(2^2\)の代数計算が実行されoutputとして”4”を得ました。
微分のやり方
微分を実行するには、diff関数を使用します。
diff(関数,微分する変数)
という形式で記述することで計算できます。
from sympy import *
x = Symbol('x')
y = sin(x)
#yをxで微分
diff(y,x)>> cos(x)今回は\(sin(x)\)を微分した結果、
アウトプットとして\(cos(x)\)を得ました。
積分のやり方
不定積分
まず不定積分の方法から説明します。
積分には、integrate関数を使用します。
integrate(関数,積分する変数)
という形式で記述することで不定積分を計算できます。
from sympy import *
x = Symbol('x')
y = E**(2*x)
#yをxで積分
integrate(y,x)>> (1/2)*E**(2*x)今回は\(e^{2x}\)を積分した結果、
アウトプットとして\(\frac{e^{2x}}{2}\)を得ました。
※不定積分定数Cは省略された形で結果が出力されることに注意。
定積分
定積分の場合には、
integrate(関数,(積分する変数,始点,終点))
という形式で記述します。
from sympy import *
x = Symbol('x')
y = E**(2*x)
#yをxで0~1の範囲で積分
integrate(y,(x,0,1))>> ((e**2)-1)/2\(e^{2x}\)を0から1の範囲で定積分した結果、
アウトプットとして\(\frac{e^{2}-1}{2}\)を得ました。
グラフ化の方法
グラフ化をするには、下のコードの様にplot関数を使用します。
from sympy import *
x = Symbol('x')
#x**2をプロットする。
#plot(関数,範囲,タイトル,x軸,y軸)の形式で記述。範囲以降は省略可。
plot((x**2),(x,-5,5),title='test',xlabel='x',ylabel='x**2')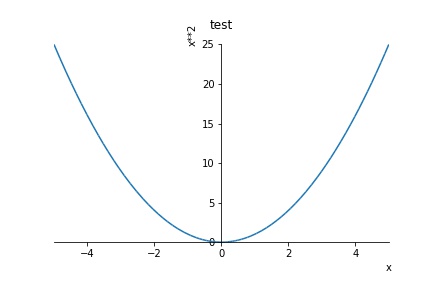
\(x^2\)を-5から5の範囲でグラフ化した結果、
上図を得ることができました。
さらに、.save(‘ファイル名’)メソッドを使うことで画像を現在ディレクトリへ保存することも可能です。
補足資料
ここでは補足として、pythonおよびsimpyライブラリで使用できる演算子、関数、定数の例を並べておきました。
ここに記載したものの他にも多数ありますが、使用頻度の高いと思われる代表的なもののみ記載しています。
演算子一覧
- 足し算(+):+
- 引き算(-):–
- 割り算(÷):/
- 掛け算(×):*
- 指数(〜乗):** ←^ではないことに注意。
関数一覧(sympy)
- サイン:sin()
- コサイン:cos()
- タンジェント:tan()
- 対数:log(変数,底) ←底は省略した場合e
定数一覧(sympy)
- 円周率(π):pi
- ネイピア数(e):E
- 無限大(∞):oo
→小文字のオーを二つ並べたもの
まとめ
sympyライブラリを使うことで簡単に代数計算ができることがお分かりいただけたと思います。
まずはコピペでコードを使ってみて、色々試していただければと思います。











コメントを書く