エクセルソルバーでの制約条件の使い方【使用例付き】

えびかずき

こんにちは、えびかずきです！

今回はエクセルソルバーの制約条件の設定方法について説明したいと思います。

制約条件の設定方法

最適化問題を解く上で非常に便利なソルバーですが、この機能を最大限に活用するためには制約条件をうまく設定することが重要です。

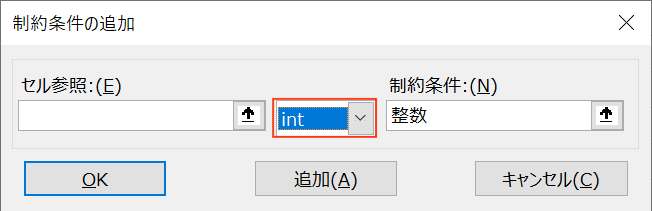
制約条件で使用できる条件は比較演算子（=,≦,≧）、整数(int)、バイナリ(bin)、All different(dif)の４種類です。

いくつかの使用例を元に、順を追って使い方を説明していきます！

設定画面の開き方

まずは、どこで制約条件を設定できるかについてです。

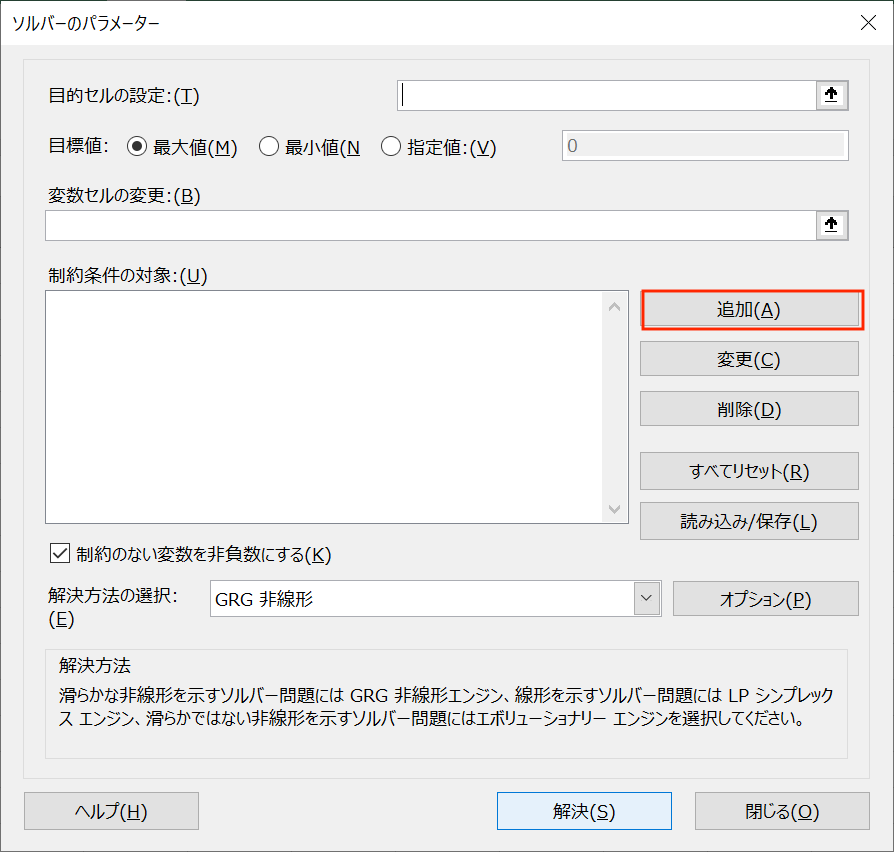
「データ」→「ソルバー」からソルバー設定画面を開いて、

赤枠の「追加」ボタンを押すことで、制約条件の設定画面を開くことができます。

比較演算子の使い方

ここからは、制約条件の使用方法についてです。

最初に比較演算子について説明します。

比較演算子は、「=」「≦」「≧」など左辺と右辺の大小関係を表す演算子のことで、

比較演算子を使えば、変数セルや目的セルに大小関係の制限を与えることができます。

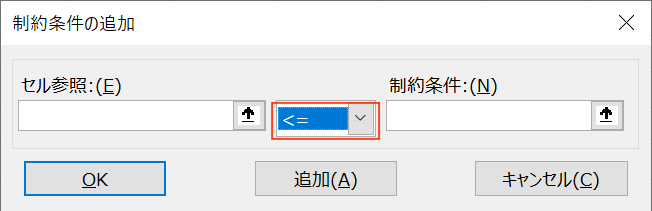
ソルバーで使用できる比較演算子は、

• ＝
• ＜＝（≦のこと）
• ＞＝（≧のこと）

の全3つになります。

※「＜」と「＞」は使えないことに注意。

連立方程式の解き方【使用例】

ここでは比較演算子で制約条件を課して、一次の連立方程式を解く例を紹介します。

$$3x­_{1}+2x_{2}+x_{3}=12$$

$$4x_{1}+x_{2}+5x_{3}=31$$

$$x_{1}+8x_{2}+2x_{3}=27$$

$$(a_{1}x_{1}+a_{2}x_{2}+a_{3}x_{3}=b)$$

という形の連立方程式を解くことを考えます。

基本的なやり方としては、

変数セルに\(x_{1},x_{2},x_{3}\)を指定し、\(b\)についてエクセルで計算した値\(b_{cal}\)と\(b_{true}\)が一致するように制約条件を与えて問題を解かせます。

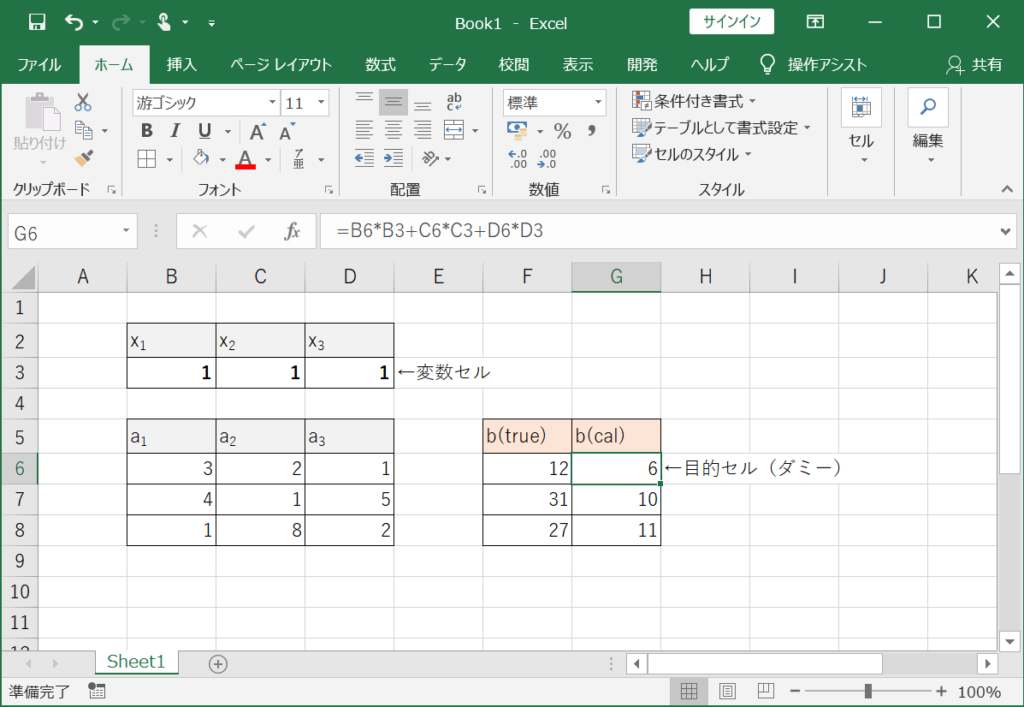
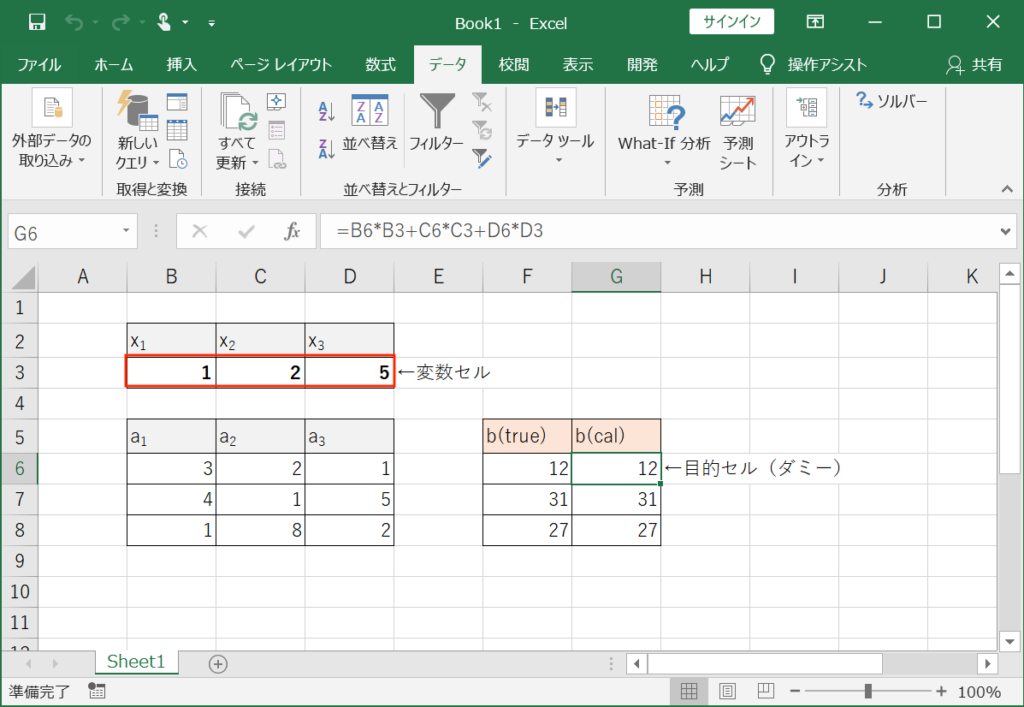
①上図のように\(x_{1}\)~\(x_{3}\),\(a_{1}\)~\(a_{3}\),\(b_{true}\),\(b_{cal}\)の入力欄を設けます。

②\(x_{1}\)~\(x_{3}\)に初期値を適当に入力します。（ここでは全て１）

③\(a_{1}\)~\(a_{3}\),\(b_{true}\)に解くべき方程式の値を入力します。

④\(b_{cal}\)にx1-x3の初期値と\(a_{1}\)~\(a_{3}\)の値を使った数式を入力します。（上図参照）

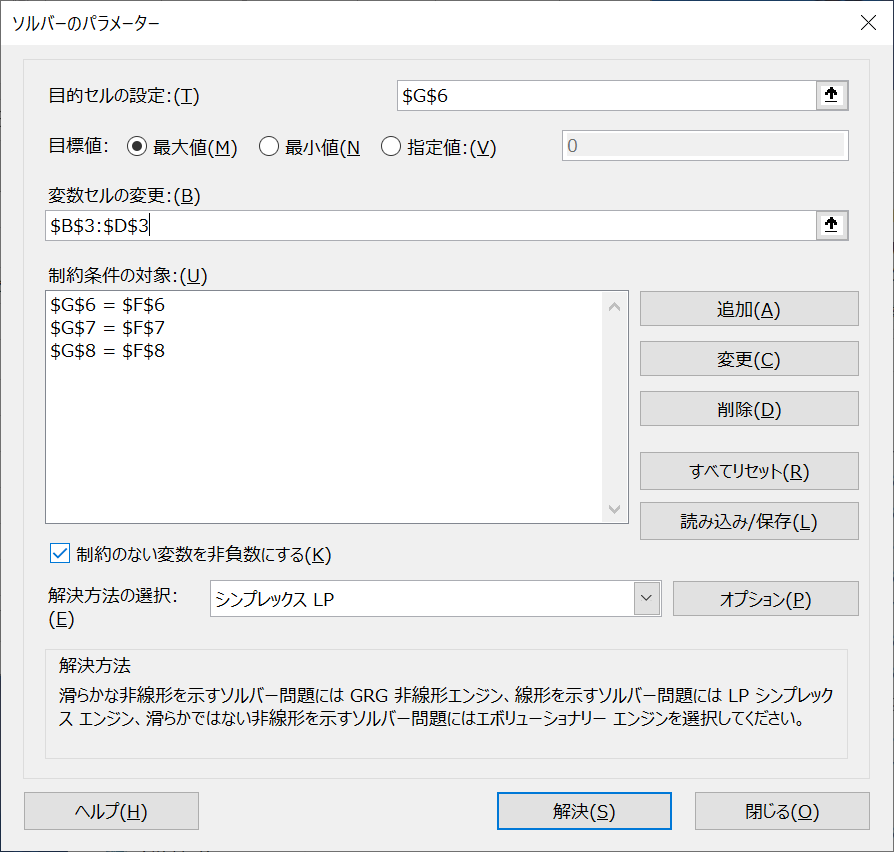
⑤変数セルに\(x_{1}\)~\(x_{3}\)の値、目的セルに\(b_{cal}\)の一つを指定します。（下図参照）

※ここで設定する目的セルはダミーで、最適化する条件は制約条件で指定します。

※最適化方法については、今回は線形問題なのでLPシンプレックスを指定します。

⑥\(b_{true}\)と\(b_{cal}\)が一致するように「=」で３つの制約条件を設定します。（下図参照）

⑦「解決」ボタンを押して最適化を実施します。

すると下の様に\(b_{true}\)と\(b_{cal}\)の値が一致して、

\(x_{1}\)~\(x_{3}\)のセルに連立方程式の解が出力されていることがわかります。

高次関数の最小値問題【使用例】

ここでは高次方程式の最小値問題を考えます。

たとえば、

$$y=x^4-2x^2+2$$

というような４次関数のyの最小値は下図の様に２点存在します。

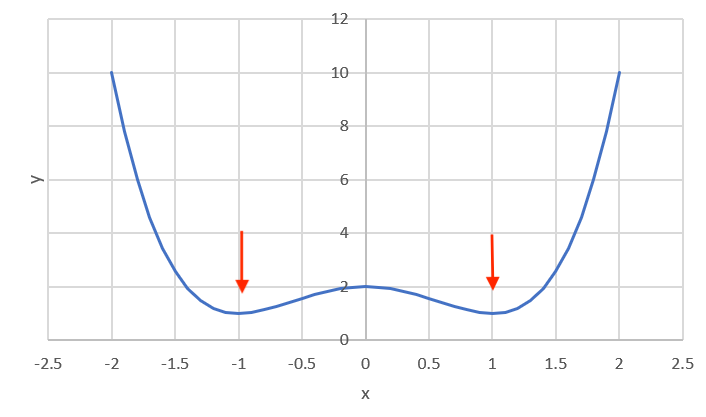
こういった場合、単純にソルバーで最適化すると変数セルに入力した初期値次第で解が変わってしまいます。

では例えば欲しい解が負の値だとする場合、どの様にすれば良いでしょうか？

①まず、係数\(a_{4}\)~\(a_{0}\),\(x\),\(y\)の入力欄を設けます（下図参照）。

②係数の値を入力し、\(x\)に適当な初期値、\(y\)に係数と\(x\)を使った数式を入力します。

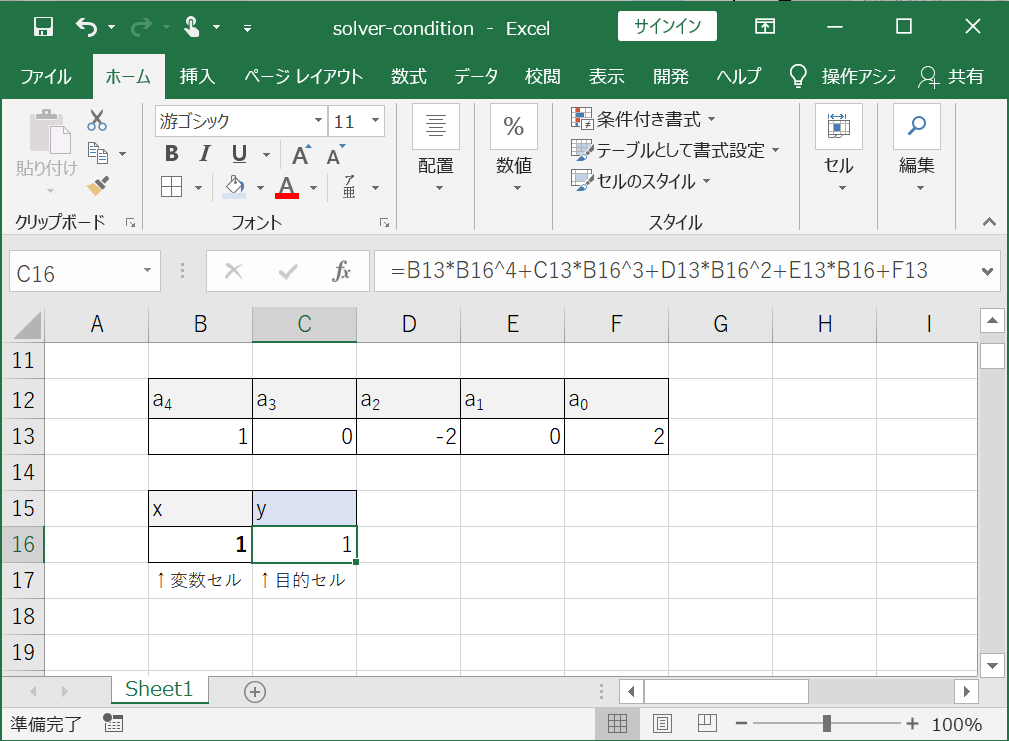
③ソルバーを開いて目的セルを\(y\)、変数セルを\(x\)と指定します。

④制約条件に、\(y\)が\(0\)以下となるように設定します（下図参照）。

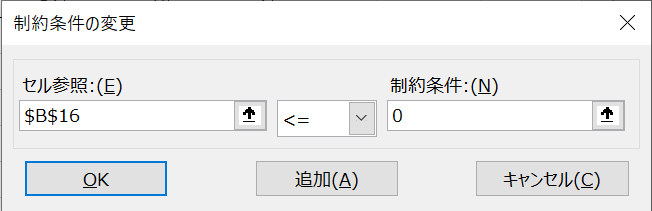
⑤解決ボタンを押します。

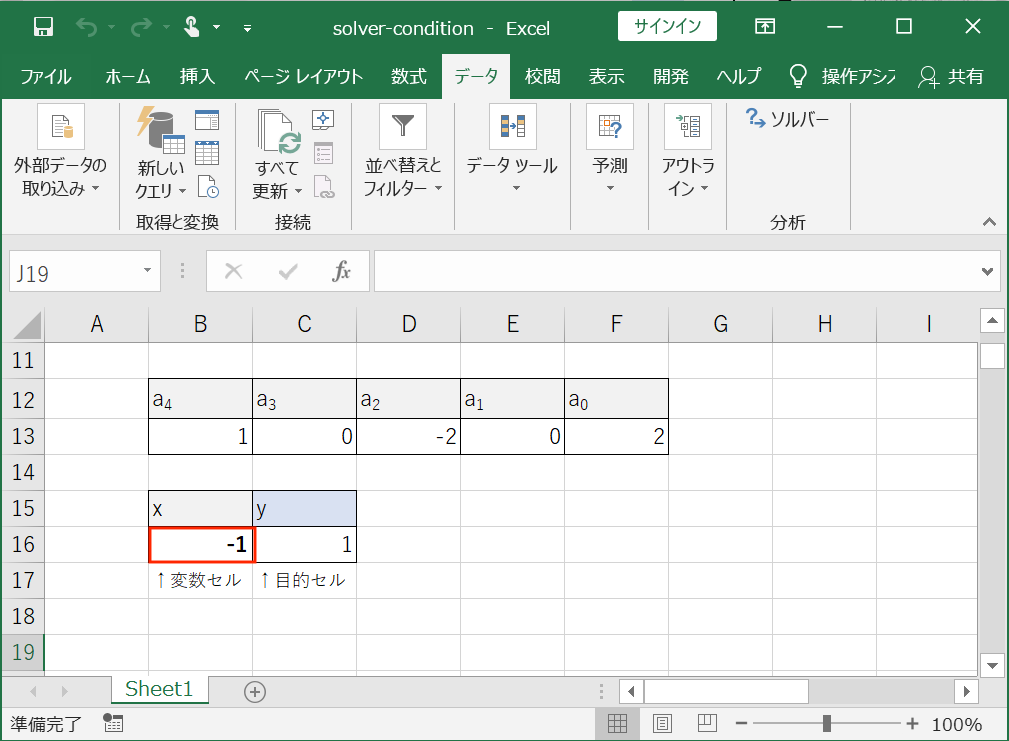
期待した通り、解は「-１」となりました。

int(整数)条件の使い方

次は、int(整数)条件の使い方についてです。

int(整数)条件は、変数セルを整数に制限できる設定です。

一万円でジュース何本買えるか？【使用例】

たとえば、

所持金1万円の時、1本147円のジュースを何本買うことができるか？

という問題を考えるとするならば、

①まずジュースの価格、購入数、総額の入力欄を設けます。

②ジュースの価格の値を入力し、購入数の初期値を適当に入力し、総額の数式を入力します。

③ソルバーの設定画面を開いて、目的セルに総額のセルを指定し、目標値を「最大値」に設定します。

④変数セルに、購入数を指定します。

⑤制約条件に、変数セルを整数に指定し目的セルを10000以下に制限します（下図参照）。

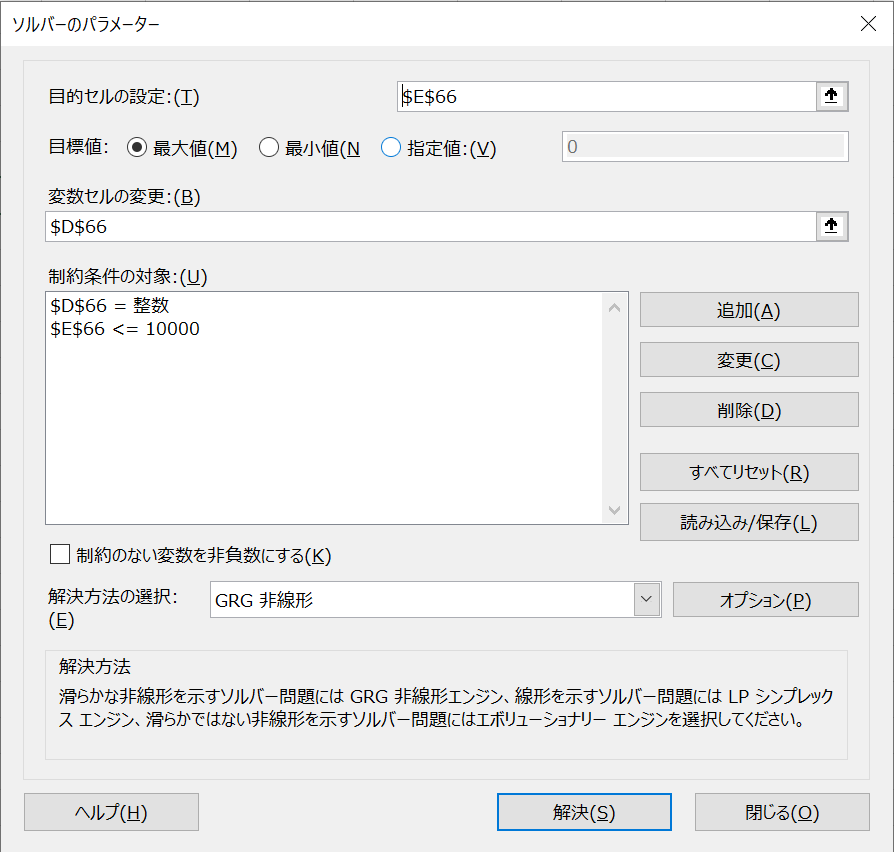
⑥解決ボタンを押します。

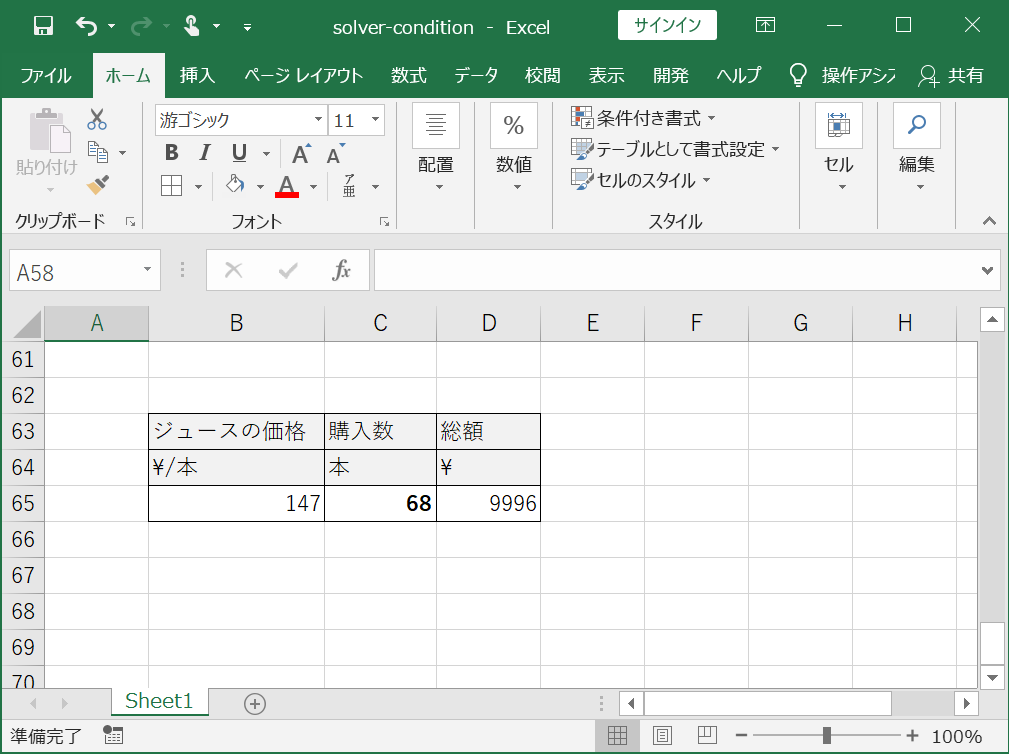
すると、68本という、整数値の解を得ることができました。

※ソルバーのオプションに

「整数制約条件を無視する」という項目が存在します。

ここにチェックが入ってしまっていると、制約条件が機能しませんのでお気をつけください。

bin(バイナリ)条件の使い方

続いてバイナリ条件について説明します。

バイナリ条件は、変数セルを「０」か「１」のどちらかにするという条件です。

この条件は組み合わせ問題などに使える条件です。

組み合わせ問題【使用例】

例えば、

下の様な果物が店頭に各一つずつ売られているとして、

所持金２千円をなるべく使い切れる組み合わせは？

• りんご¥156
• みかん¥124
• もも¥384
• なし¥288
• いちご¥521
• ぶどう¥732
• さくらんぼ¥482
• マンゴー¥821

という問題を考えるとします。

こういった組み合わせ問題は、確認すべき組み合わせが膨大な数になるため、コンピュータで解くことが有効です。

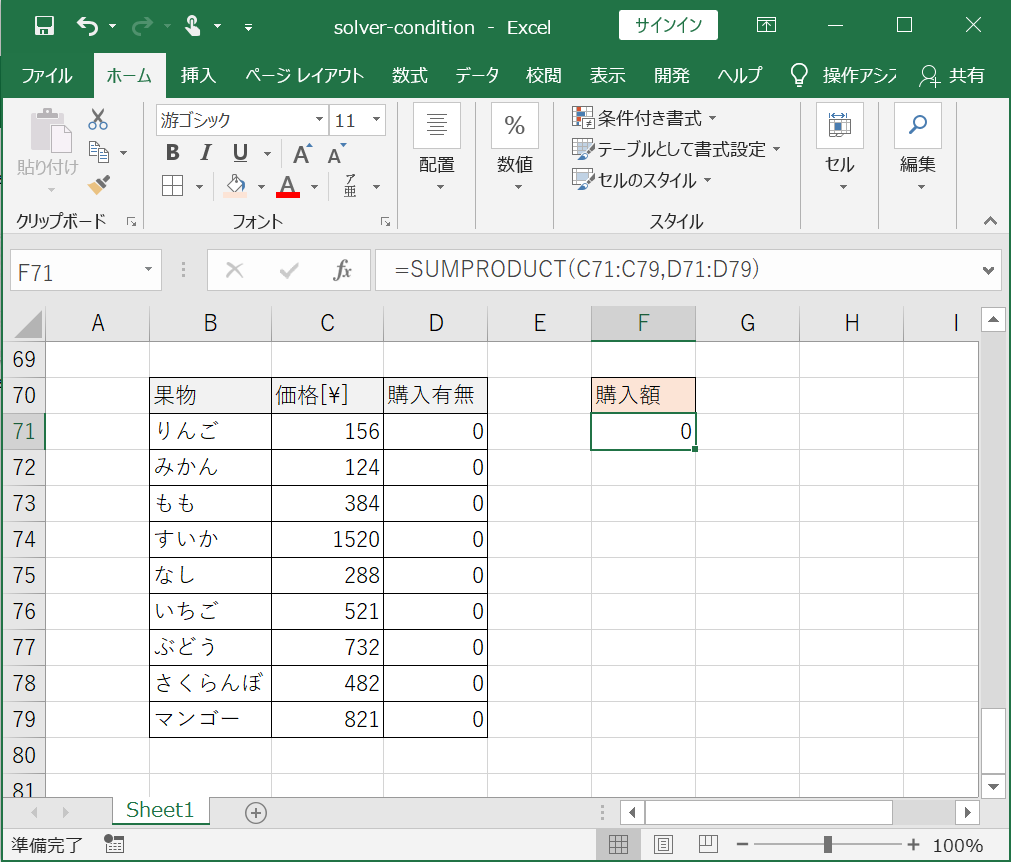
①まず、各果物の価格と購入有無を入力する欄を設けます（下図参照）。

②果物の価格を入力し、購入有無にひとまず初期値として「０（買わない）」を入力します。

③購入額に「SUMPRODUCT」関数を使って、購入した総額を算出する数式を入力します。（下図参照）

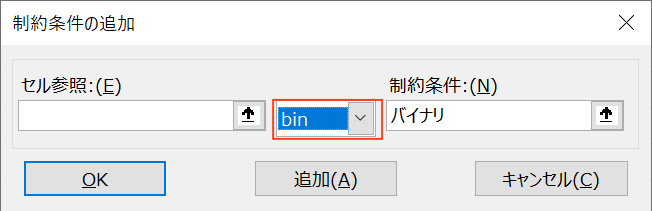
④ソルバーを開いて、目的セルに購入額、変数セルに購入有無のセルを指定し、目標値を最大値とします。

⑤制約条件にて、購入有無をバイナリに指定し、購入額を２千円以下に制限します。

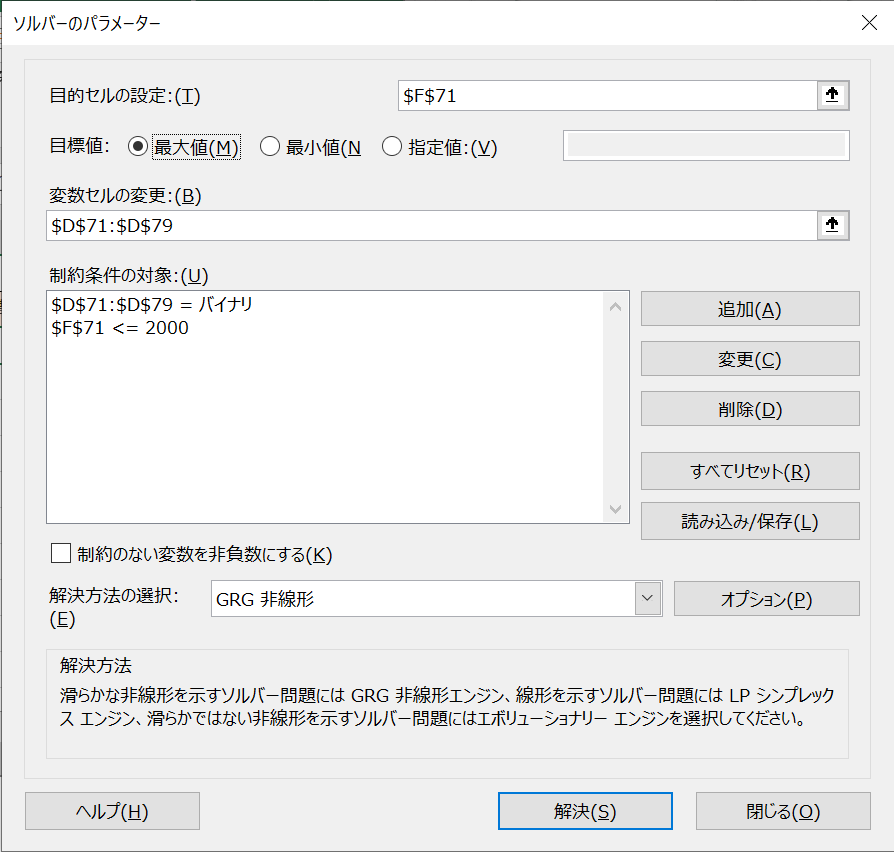
⑥解決ボタンを押します。

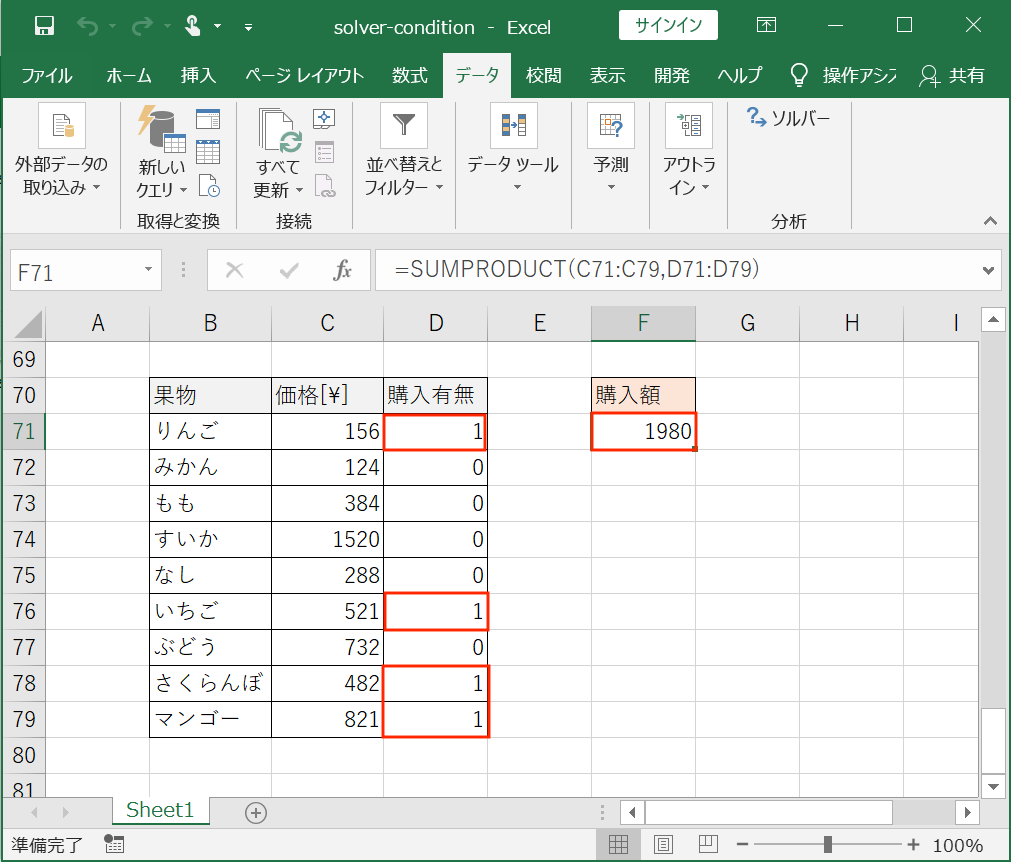
すると、

りんご、いちご、さくらんぼ、マンゴーの組み合わせの場合が1980円となり、最適であることがわかりました。

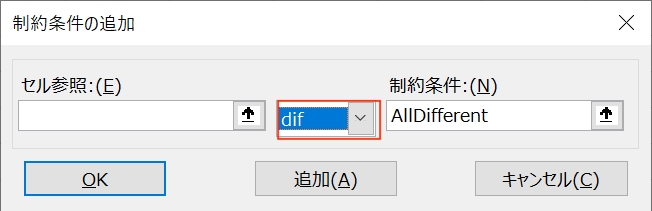
dif(All different)条件の使い方

dif(All different)条件は、指定した変数セル（N個）に、1~Nの値を割り当てるという条件です。

これは組み分け問題などに応用できる条件です。

組み分け問題【使用例】

たとえば、

それぞれの体重がわかっているクラスの男子１２名（A〜H君）を４組に分けて綱引きトーナメントを実施する場合の最適な（体重のばらつきが最小な）組み分け方は？

という問題を考えるとします。

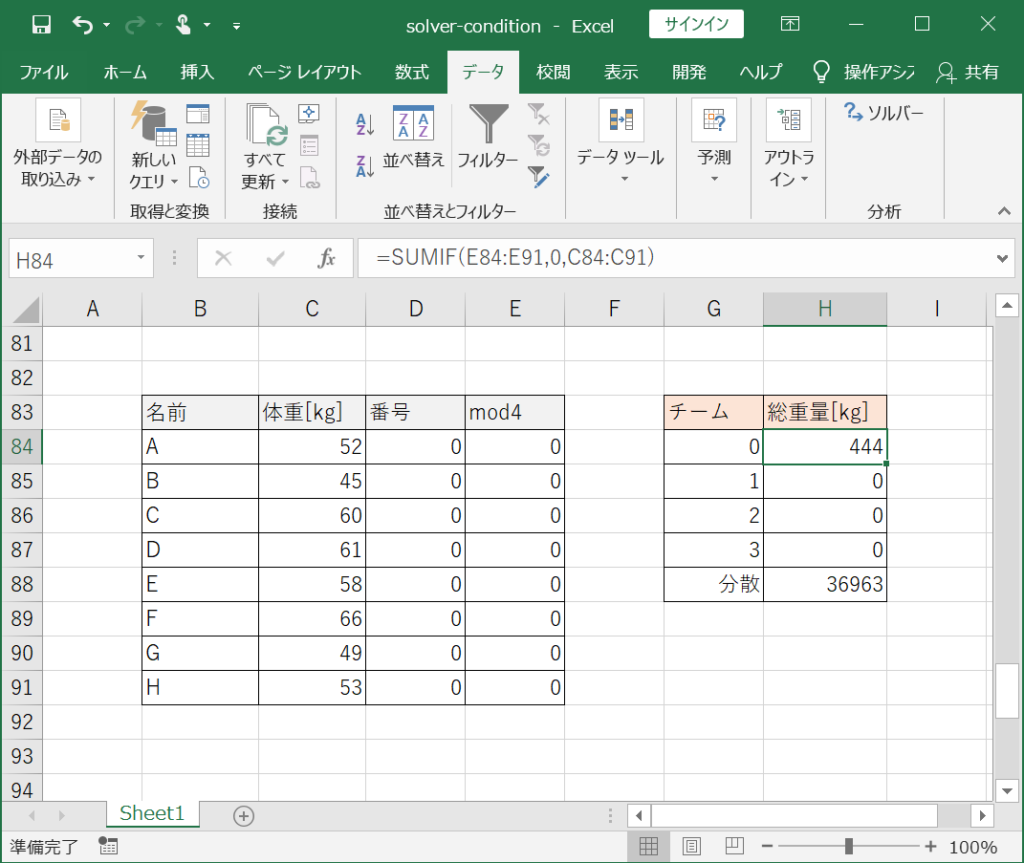
①A〜H君それぞれの体重、番号、mod4の入力欄と、各チーム（0〜4）の総重量、分散の入力欄を設けます。（下図参照）

②下の要領で各セルへ数値を入力します。（下図参照）

• 体重：A〜H君の体重
• 番号：初期値として全て０（変数セル）
• mod4：番号のセルの4で割った余りを算出する数式「＝１MOD（番号）」
• チーム：0〜4(mod4の数値に対応)
• 総重量：各チームの総重量をSUMIF関数を使い数式として入力
• 分散：VAR.P関数を使って、４チームの総重量の分散（ばらつき）を出力する数式を入力する。（目的セル、ここが小さいほどばらつきが小さい）

③ソルバーを開いて、目的セルに分散、目標値を最小値、変数セルに番号を指定する（下図参照）。

④制約条件として、番号をAll differentとします（下図参照）。

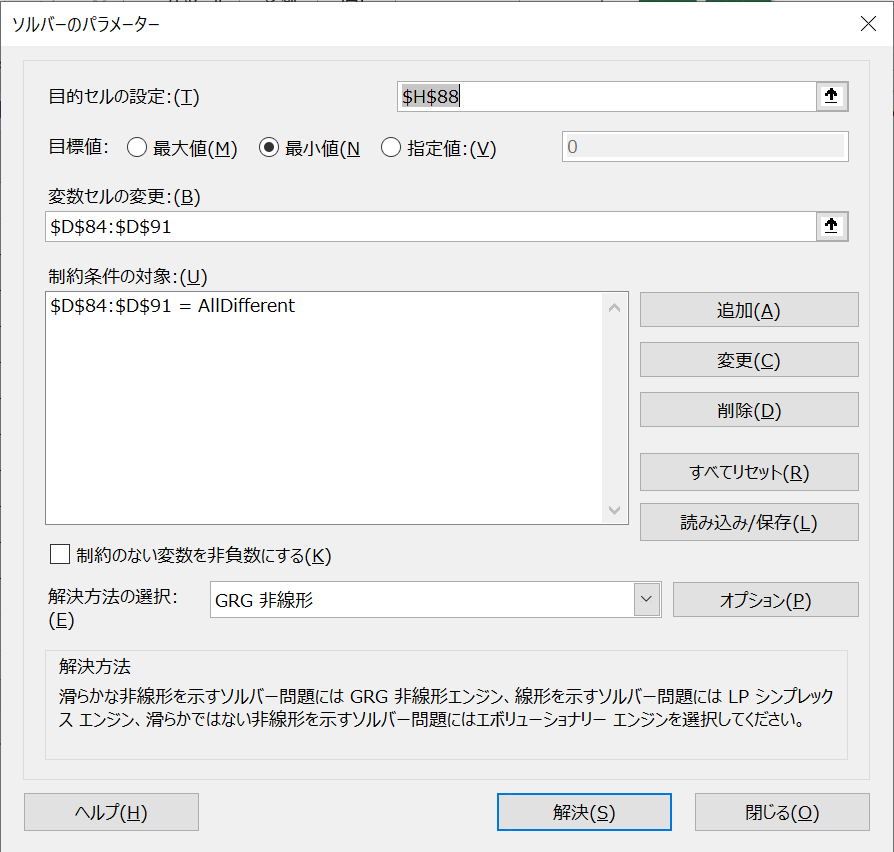
⑤解決ボタンを押します。

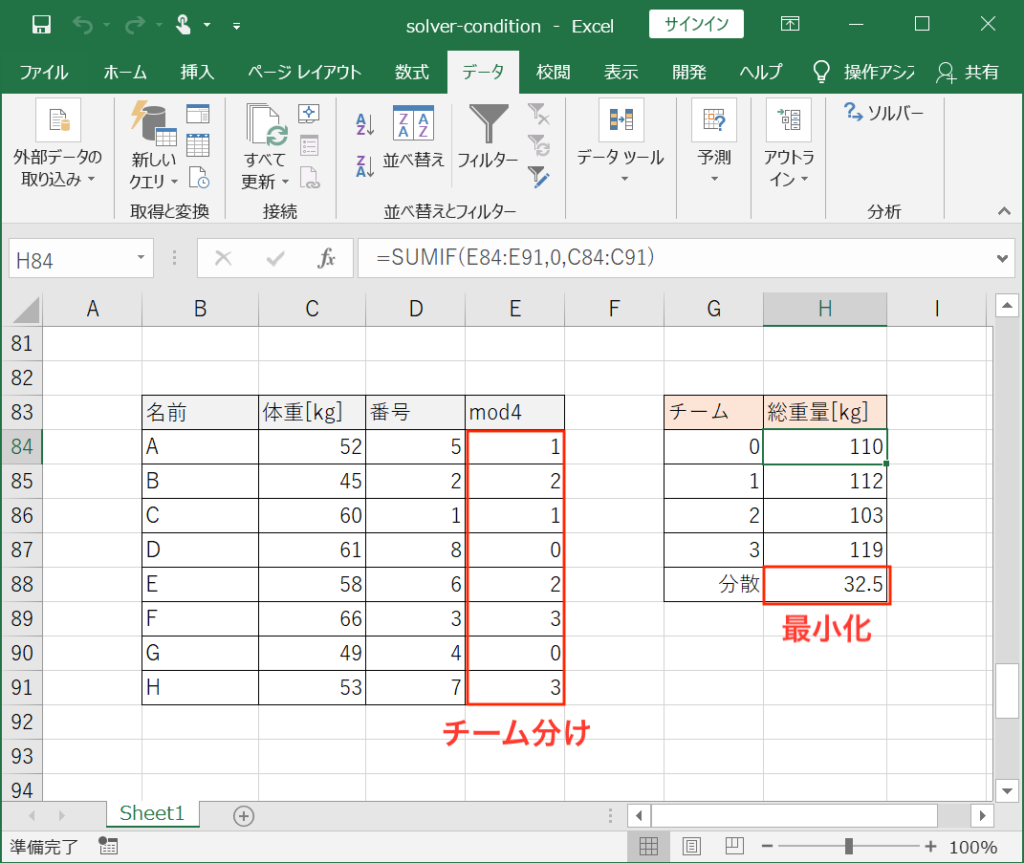
すると、ばらつきが最小となるチーム分けの結果が出力されます。

さすがにこういった問題はPCでなければ解くことが出来ないでしょう。

動作確認環境

• Windows/Excel2016 (ver.1908)
• Windows/Office365 (ver.1908)
• Mac/Excel2016 for mac (ver.190811)

※説明及び使用している画像は、主にWindowsでのExcel2016になります。

まとめ

今回はソルバーの使用例を紹介しつつ、制約条件の使い方について説明しました。

うまく制約条件を設定することで、連立方程式や組み合わせ問題、組み分け問題などなど、エクセルで様々な問題が解けるということがわかりました。

もしみなさんの仕事や職場で応用できる例があれば、ぜひ使ってみてください！