Pythonは素数を1時間で何個見つけられるか？

えびかずき

こんにちは、えびかずきです。

今回はPythonで素数の計算を1時間やってみました！

今回はいつものHow-To系の記事から趣向を変えて、

Pythonで素数をひたすら計算させるというチャレンジをやってみました。

結果として、約80万個の素数を見つけることができました。

開発環境

PC：MacBook Pro /Mid2014
プロセッサ：2.6 GHz デュアルコアIntel Core i5
メモリ：8 GB 1600 MHz DDR3
OS：MacOS Catalina10.15

Python3.7.3
numpy
matplotlib

計算プログラム

今回使った計算プログラムは、とても単純です。

ある数pを2,3,4,…と順番に割って、√pまで余りが出なければ、pは素数であるといえます。

これをp=3,4,5,6,…と一つづつ数を大きくして確かめていきます。

# 素数計算のプログラム

from numpy import sqrt
import time
from matplotlib import pyplot as plt

# 素数リストに最初の２だけ入れておく
p_list = [2]
#計算時間リストに最初の0だけ入れておく（単位は秒）
t_list = [0]
start_time = time.time()

# pが素数を表す
for p in range(3,30000000):
    
    frag = True
    #2から順番に割り切れるかどうかを試す。
    #√pまで一つも割り切れるものがなければpは素数。
    for i in range(2,int(sqrt(p))+1):
        if p % i == 0:
            frag = False

    if frag:
        p_list.append(p)
        t_list.append(int(time.time()-start_time))

    if t_list[-1] > 3600:
        break

# プロットの準備
x = t_list
y = p_list

# グラフの描画
plt.plot(x, y)
plt.show()

# 最終結果の出力
print('見つけた個数：',len(p_list))
print('最大の素数：',p_list[-1])

        

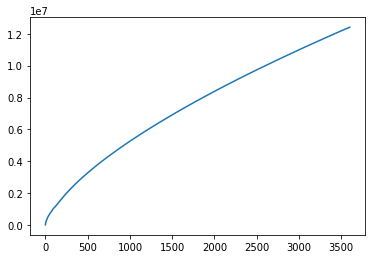
計算結果

約80万個という途方もない数の素数を発見することができました。

だから何？という話ですが、ただやってみたかっただけです。笑

最大の素数については、かつて数学界の伝説オイラーが手計算でn=31のメルセンヌ数が素数であることを証明した言われています。

\(2,147,483,647（=2^{31}-1）\)

このあたりを超えてくるとうれしかったですが、なかなか総当たりの単純なプログラムでは手の届かない数のようです。

PCの力をかりたとはいえ、力づくの計算ではダメですね。

計算の過程

下のグラフは計算時間[s]に対して、発見した素数をプロットしたものです。

やはり数が大きくなるにつれて確認作業に時間がかかり、曲線がねてきているのがわかりますね。

iPhoneを使った場合（おまけ）

最後におまけで、iPhoneで計算するとどうなるかを試してみました。

環境：
iPhone8
Pythonista3

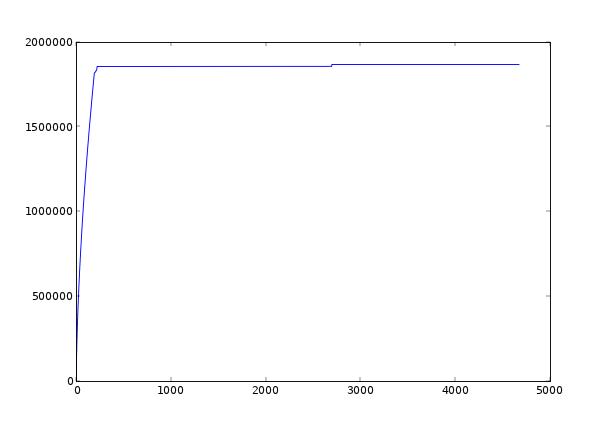
結果は約14万個ということで、
PCの場合の五分の一程度しか素数を発見できませんでした。

ただしこれはiPhone8がPCの５分の1の性能だからというわけではなさそうです。

なぜなら計算の過程を確認してみると、最初の約３００秒だけちゃんと計算をして、それ以降は計算が著しく遅くなっています。

iPhone画面が落ちてスリープモードに入ると計算をわざと遅くしているのかもしれません。

まとめ

今回は、Pythonを１時間走らせて素数が何個みつかるかを試してみました。

コードはそのまま使えると思うので、みなさんの環境でどうなるが試してみても面白いかもしれません。