こんにちは、えびかずきです。
今回はK-means法をscikit-learnで使う方法について説明していきます。
こんな人におすすめ:
・K-means法をscikit-learnで実装したい
・教師なし学習について学びたい
結論として、scikit-learnでK-means法を実装するのは極めて簡単で、sklearn.clusterモジュールのKMeansクラスに学習させるデータとクラス分けの数を入れるだけです。
ここでは、実装手順に加えてK-means法の原理についても簡単に説明していきます。
それでは順を追って説明していきます。
開発環境
Python 3.7.3
scikit-learn 0.24.2
Pandas 1.2.4
seaborn 0.11.1
IDE:jupyter Notebook
K-means法の使い方
今回もscikit-learn.datasetsのiris(アヤメ)のデータサンプルを使って実装していきます。
まず、irisのデータをロードしてPandasでデータフレーム化します。
from sklearn.datasets import load_iris
iris = load_iris()
import pandas as pd
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['target'] = iris.target
df.loc[df['target'] == 0, 'target'] = "setosa"
df.loc[df['target'] == 1, 'target'] = "versicolor"
df.loc[df['target'] == 2, 'target'] = "virginica"
df.head()
irisのデータには品種のラベルがついています。
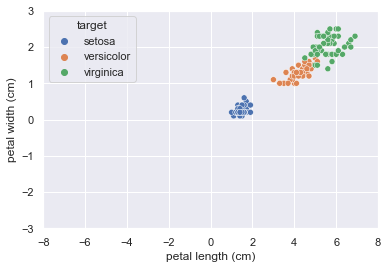
横軸にpetal_length(花びらの長さ)縦軸にpetal_width(花びらの幅)をとってプロットしてみましょう。
import seaborn as sns; sns.set()
sns.scatterplot(data=df, x='petal length (cm)', y='petal width (cm)', hue='target')
import matplotlib.pyplot as plt
plt.xlim(-8, 8)
plt.ylim(-3, 3);その結果がこちら。
花びらのデータによって3つのクラスターに分かれていることが見て取れます。
それではここから、K-means法を試していきましょう。
K-means法でクラスタリングした結果が上のラベル付きデータをプロットした図と一致すれば分類は成功です。
K-means法はsklearn.clusterモジュールのKMeansクラスをつかって以下のように実装します。
ここで注意すべきことは、分けるクラス数はあらかじめ決めておかなければならないということです。
今回は3つのクラスターに分けたいので、3を入れます。
from sklearn.cluster import KMeans
X = iris.data[:, [2, 3]]
kmeans = KMeans(n_clusters=3)
kmeans.fit(X)
kmeans.labels_クラスター分けの結果がこちら。

これではわかりずらいので、データフレームを書き換えて図示していきましょう。
df["target"] = kmeans.labels_
df.head()
import seaborn as sns; sns.set()
sns.scatterplot(data=df, x='petal length (cm)', y='petal width (cm)', hue='target')
import matplotlib.pyplot as plt
plt.xlim(-8, 8)
plt.ylim(-3, 3);K-means法でラベリングした結果を図示したものがこちら。
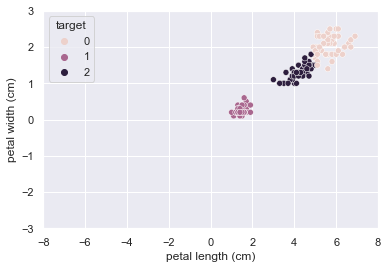
図1と見比べてみると、ほとんど一致していることがわかりますね。
分類は成功といってよいでしょう。
K-means法の原理
K-means法の原理を簡単に説明すると、クラスターがK個あるとした時、それぞれのクラスターの平均ベクトルを代表点として、各データとの距離の二乗和が最小になるように最適化したクラスタリング手法です。
概念としては、ちょうど教師あり学習の最近傍法と似ています(最近傍法は”二乗でない”距離を指標として教師あり学習をする)。
数式で表すと最適化する評価関数Jは、
\(\displaystyle J(q_{ik},\textbf μ_k)=\sum_{i=1}^N \sum_{k=1}^K q_{ik}||\textbf x_i-\textbf μ_k||^2\)
\(x_{i}\):i個目の学習データ、\(\textbf μ_k\):k番目のクラスターの平均ベクトル、\(q_{ik}\):クラスターの帰属変数(\(x_{i}\)がk番目のクラスターに属している時1,それ以外は0)
||・||はノルム(ベクトルの長さ)を表す記号と
とします。
すなわち、このJの値が最小になるように学習データごとの\(q_{ik}\)と各クラスターごとの平均ベクトル\(\textbf μ_k\)を選べば良いということになります。
しかしながらこの最適化が一筋縄ではいきません。
残念ながら\(q_{ik}\)と\(\textbf μ_k\)を一度に最適化することは不可能なので、まず初期値として\(\textbf μ_k\)を適当に決めてしまって、それを元にJが最小になるよう\(q_{ik}\)を決めて、再度\(\textbf μ_k\)を計算して・・・と繰り返し最適化をすすめます。
最終的に\(\textbf μ_k\)にズレがなくなれば終了というわけです。
段階的に最適化していく様子は、数式だと少しイメージしづらいですが、以下のサイトにわかりやすいイメージ図があったので参考になると思います。
また、記事下部の参考書籍「Pythonではじめる機械学習」のGithubリポジトリにもわかりやすい図がありましたので参考になると思います。
K-means法の特徴
K-means法は教師なし学習におけるクラスタリングの代表例ともいえる手法です。
クラスタリングにおいては、まず初めにk-means法を試してみようというような位置付けです。
一方で、k-means法はクラスターの重心を元に最適は進めていく学習方法なので、複雑な形の分布をしたクラスターの分類には向きません。そういったケースでは、類似したデータを繋げてクラスターを作っていくような融合法を使ったクラスタリングだとうまくいく場合があります。
ちなみに、教師あり学習にk-最近傍法という手法がありますが、それとK-meansは別物ですのでお気をつけください。
そもそもKの意味が違っていて、K-meansのKはクラス数のことを表していますが、k-最近傍法のkは多数決を取る周囲のデータ数の数のことを言っています。
k-最近傍法については過去記事で紹介していますので参考まで。
まとめ
今回はk-means法をscikit-learnで使う方法について説明しました。
k-means法は概念自体は割りと簡単で、本質的には教師あり学習の最近傍法と同じくデータ間の距離を指標にしてクラス分けの空間を作るというイメージです。
しかしながら、しっかりと中身を理解しようとすると最適化の仕組みが意外と面倒で、段階的に最適化していくというところが少し理解しづらい点かと思います。
この記事が少しでも理解の助けになれば幸いです。
また、scikit-learnによる実装は極めて簡単で、2~3行のコードでかけてしまうので、実際中身をよくわかっていなくても使えてしまうのが実情です。
しっかり中身を理解して、k-means法の用途を見極めましょう。
参考
記事作成にあたって、以下の書籍が参考になりました。











コメントを書く