なぜ多くのデータは正規分布を示すのか？【二項分布との関係】

こんにちは、えびかずきです！

統計データを扱うときに正規分布に従うという仮定をおくことが多いと思いますが、

「本当に良いのかな？」と疑問に思ったことはありませんか？

結論としては、

偶然のバラツキに由来するたいていのデータは正規分布で仮定してOKです。

なぜなら正規分布は、二項分布（あるいはガウスの公理）から自然と出てくる関数だからです。

ではこの内容について詳しくみていきましょう！

1. 正規分布とは
2. 正規分布は二項分布から導ける
- 2.1. 正規分布と二項分布の類似性確認
- 2.2. 二項分布（n大）と正規分布が一致する意味
3. 正規分布はガウスの公理からも導ける
4. まとめ
5. グラフの実装コード（python3）
6. 開発環境
7. 参考

正規分布とは

正規分布とは下式で示される確率変数xの確率密度を返す関数です。

正規分布：

\(N(μ,σ^2)=\dfrac{1}{\sqrt{2πσ^2}}\exp{-\dfrac{(x-μ)^2}{2σ^2}}\)

なんだか複雑だけど、こんな関数どうやって出てきたんだ？

と思いますよね。

実はこの関数、二項分布との関係が深いのです。

なんと正規分布は、nが十分に大きい場合の二項分布で近似することができるんです！

正規分布は二項分布から導ける

ここでは、正規分布が二項分布で近似できるということについて見ていきます。

二項分布とは、

ある確率pでおこる事象をn回試行（ベルヌーイ試行）した場合に、

実際に発生した回数xの確率分布のことです。

例えばn回コイン投げをして表が出る回数をxとした場合に、

xの確率分布はどうなるかというものです。

例としてコイン投げを10回した場合のグラフが以下です。

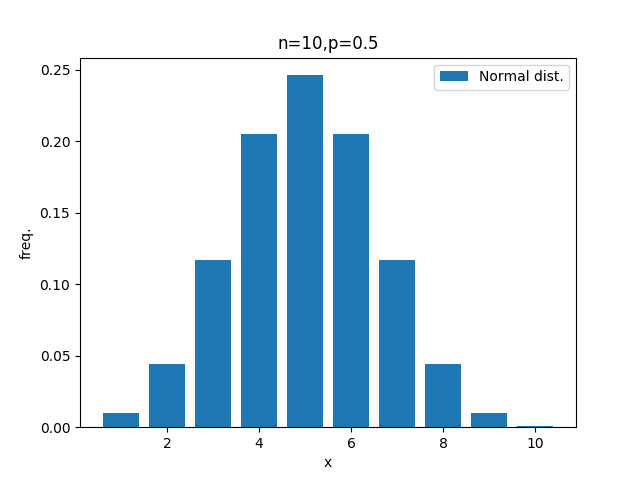
上の図は感覚とも一致するのではないかと思いますが、

コインを10回投げると表が5回(x=5)となる確率がもっとも高い釣鐘状の分布となります。

さて本題ですが、この分布は下式の二項分布の式で表すことができます。

二項分布：

\(B(n,p)=_nC_x p^x (1-p)^{n-x}\)

ここで重要なのが、

nが十分大きければ、二項分布B(n,p)は下式のN(np,np(1-p))に近似できる

ということです。

\(N(np, np(1-p))=\dfrac{1}{\sqrt{2πnp(1-p)}}\exp{-\dfrac{(x-np)^2}{2np(1-p)}}\)

この二項分布と正規分布の関係は、ド・モアブル-ラプラスの定理と呼ばれています。

ここでは証明は割愛しますが、詳しい証明を知りたい方は、

下部の参考欄にリンクを貼っていますので参考にしてください。（中身は数学になれてないとちょっと苦しいかもしれません。）

正規分布と二項分布の類似性確認

nが大きい時に両者が本当に一致するのか、

pythonのmatplotlibでグラフ化して確かめてみましょう！

まずn=10の場合。

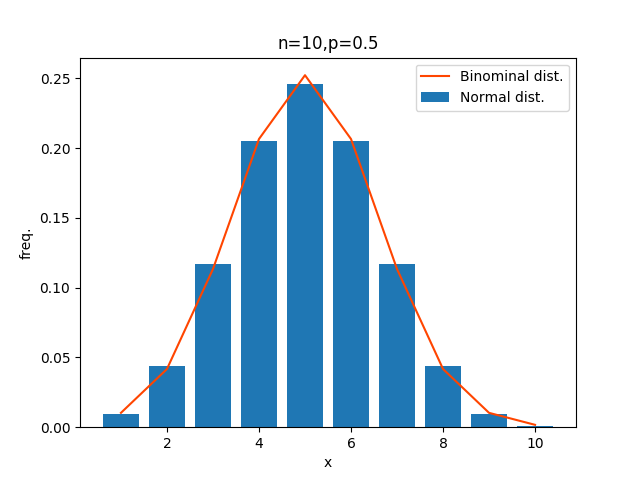
n=10と割と小さい数でも、ほとんど一致してしまっています。

次にn=30。

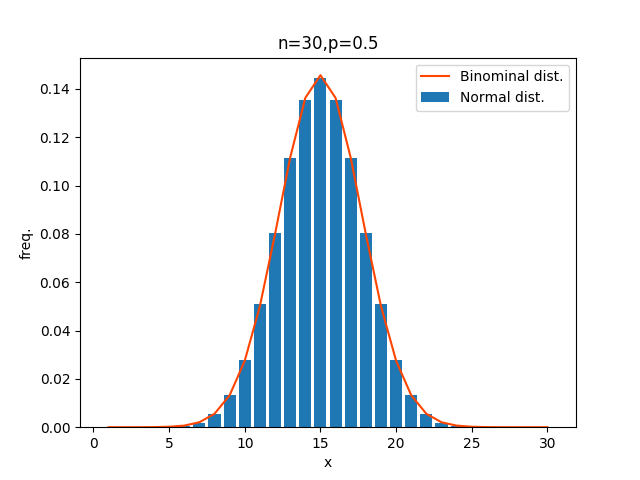
n=30にするとさらに一致度が高くなっていそうですね。

最後にn=300。

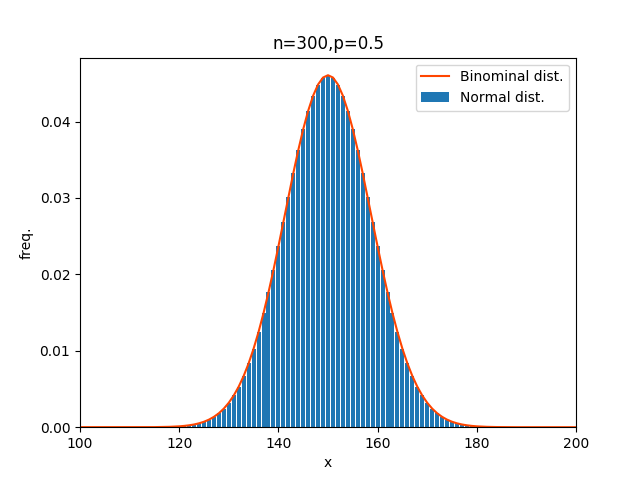
n=300までくると、両者はほぼ一致していますね。

二項分布（n大）と正規分布が一致する意味

二項分布はある確率pで偶然に起こるある事象の発生回数xの分布ですが、

われわれが普段扱う統計データも、

ある確率で偶然に起こる”ある事象”のたくさんの重ね合わせで表現されていると考えると、

二項分布と正規分布が一致することに納得ができます。

正規分布ただの経験則からできた関数というわけではなく、

見つかるべくして見つかった関数なのです。

正規分布はガウスの公理からも導ける

実は他にも正規分布を導く方法があります。

それはガウスの公理（前提とする約束）から導くという方法です。

ガウスの公理：

1.大きさの等しい正と負の誤差は等しい確率で生じる。
2.小さい誤差は大きな誤差より起こりやすい。
3.ある限界値より大きな誤差は実際上起こらない。
http://www.eng.niigata-u.ac.jp/~nomoto/7.html

簡単なこれら３つの公理を認めるという前提の下、正規分布を導くことができます。

こちらも証明は長くなるので割愛しますが、

詳しい導出方法は参考の欄にリンクを貼りましたので、中身を知りたい方は参考にしてください。

このことからもやはり正規分布は、ばらつきのあるデータの分布を仮定する上でまともな関数と言えそうですね。

一言メモ：
正規分布はガウス分布とも呼ばれていて、19世紀の有名な数学者ガウスが大きな貢献をしたことに由来しています。
（正規分布の発見者については諸説あるようですが。）

まとめ

今回は、統計データを正規分布で仮定するというのが妥当なのかどうかについて説明しました。

正規分布は二項分布とガウスの公理から自然と導けることからその妥当性を理解できます。

これからは自信をもって正規分布を使っていきましょう！

グラフの実装コード（python3）

おまけとして、説明で使ったグラフの実装コードを添付しておきます。

グラフで遊んでみたい方はどうぞ。

#グラフ化の実装コード
import matplotlib.pyplot as plt
import numpy as np
from  math import factorial as fact,pi,exp

#Binominal dist.
def cmb(n,r):
    return fact(n) // fact(r) // fact(n - r)
def Bi(n,p,x):
    return cmb(n,x)*p**x*(1-p)**(n-x)

n = 100
#n = 30
#n = 100
#n = 300
x = n
p = 1/2
left = []
height = []

for i in range(1,x+1):
    left.append(i)
    height.append(Bi(n,p,i))

plt.bar(left,height,label="Normal dist.")

#normal dist.
x_axis = []
y_axis = []

def N(m,s,x):
    return (1/((2*pi*s)**(1/2))) * exp(-((x-m)**2)/(2*s))

for i in range(1,1+x):
    x_axis.append(i)
    y_axis.append(N(n*p,n*p*(1-p),i))

plt.plot(x_axis,y_axis,color="orangered",label="Binominal dist.")

#グラフの表示
plt.title('n='+str(n)+',p='+str(p))
plt.ylabel('freq.')
plt.xlabel('x')
#範囲指定
#plt.xlim(1/3*x,2/3*x)
plt.legend()
plt.show()