こんにちは、えびかずきです。
突然ですが、問題です。
コインを20回投げて15回表が出た時、このコインはまともだと言えるか?
こんな問題に出会った時、みなさんはどうやって解決しますか?
ここで活躍するのが仮説検定です!
では具体的な方法について解説していきます。
仮説検定の例1
細かい解説は後にまわすとして、まずは先ほどの問題を実際に解いてみましょう!
問題:
コインを20回投げて15回表が出た時、このコインはまともだと言えるか?
①まず帰無仮説を設定する
仮説検定は、ちょうど数学の背理法と似たような考え方です。
間違いとしたい仮説(帰無仮説)を前提に話を進めて、矛盾を導くという手法になります。
ここでは、帰無仮説を、
帰無仮説:
「表が出る確率pが1/2である。」
に設定しましょう。
②帰無仮説を前提に確率を求める
つづいて、設定した帰無仮説を前提に確率を具体的に計算します。
ここで考えているコイン投げの確率は、二項分布で計算できます。
具体的には下の式で表すことができます。
二項分布:
\(B(n,p)=_nC_x p^x(1−p)^{n−x}\)
n:コイン投げの回数、p:表が出る確率(=1/2)、x:表が出た回数
とりあえずここでは式の意味を理解してなくても大丈夫です。
次に進みましょう。
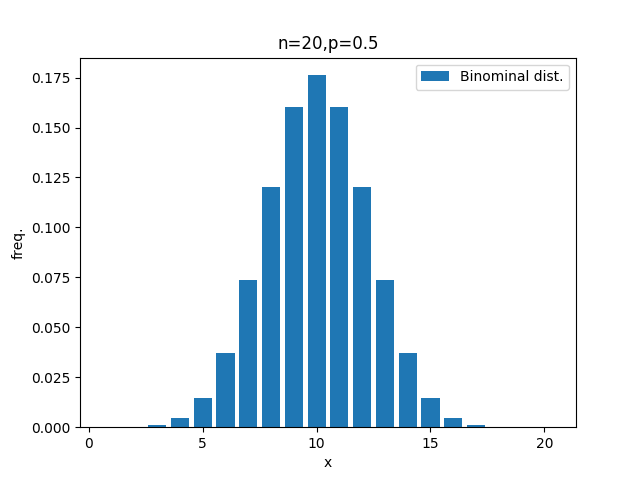
結果は以下のようなグラフになります。
これをみると、p=1/2のコインを20回投げた場合、
平均値が10回の釣鐘状の分布を示すことがわかると思います。
③有意水準を設定する
有意水準とは、
帰無仮説が間違いだと判断するために使う確率の基準値のことです。
これは適切な数値を自分で決める必要があります。
例えば有意水準を5.0%に設定する場合、
帰無仮説が起こる確率がこれより小さければ、帰無仮説が間違いであると言えるわけです。
有意水準は危険率と呼ばれることもあります。
結論を出す時に、
結論:
帰無仮説は危険率5%で棄却された。
とかいう言い回しをすることがあるのですが、この場合には危険率といった方がしっくりきますね。
④p値と有意水準を比較する
p値とは、帰無仮説を前提とした場合に今考えている事象が起こる確率(probability)のことをいいます。
今考えているのは、20回中15回以上もコインが表になる場合なので、
p値は下図の赤枠の領域を考えます。
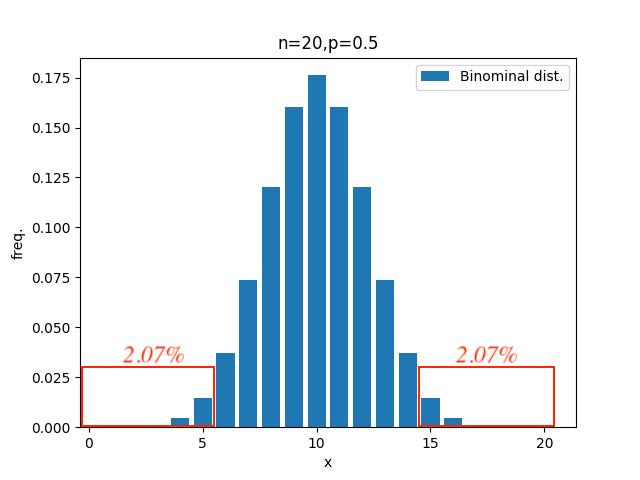
15回以上の領域と、さらに5回以下の反対側の領域も加えて、p値は約4.1%です。
※なんで5回以下の確率もp値に入れちゃうの?
という疑問には後の両側検定に関する説明のところでお答えします。
⑤結論を出す
上の手順より
帰無仮説として設定したp=1/2という状況では、20回中15回も表が出るなどという現象は、
p値4.1%という有意水準5.0%より小さい確率でした起こり得ないので、
このコインまともとは言えない。
という結論を出すことができます。
これで仮説検定は終了です。
仮説検定の手順
だいたいの流れは上の説明でつかめたと思いますが、手順をおさらいをしましょう。
まとめると下のような手順になります。
①帰無仮説を設定する
②帰無仮説を前提として確率を計算する(p値を出す)
③有意水準を設定する(一般的には5%,1%,0.1%などが選ばれる)
④p値と有意水準を比較する(つまりp値<有意水準を示す)
⑤結論を出す(出すべき結論は「帰無仮説は正しいとは言えない」ということ)
注意:
仮説検定は背理法と違って厳密に証明できているわけではないことに注意が必要です。
あくまでも設定した有意水準(危険度)での条件付きで結果を解釈するということを忘れてはいけません。
両側検定と片側検定
仮説検定では、両側検定と片側検定のどちらを実施するかを選ぶ必要があります。
そしてその違いは、
p値として確率分布の両側を取る(両側検定)か?
それとも一方の片側だけ(片側検定)とするか?
どちらにするかは場合によりますが、結論としたい主張(対立仮説)を考慮すると良いです。
今回結論としたい主張(対立仮説)は、
対立仮説:
コインがまともでない(つまりp≠1/2)
です。
ということは、
逆に表が全然出ない側が発生する場合についても、”まともでない”に該当するため、両側検定を使いました。
有意水準の設定値について
両側検定で有意水準5.0%と設定するような場合、片側検定では作為的にならないようにその半分の2.5%を使ったりします。
が、有意水準をいくらにするかは結局のところ検定をする人しだいです。
有意水準は納得感のある結論を導けるように、場合に応じて適切に設定しましょう。
仮説検定の例2
最後にもう一例紹介しようと思います。
解きたい問題は、
問題:
スーパーで500mLパックに入った「誠実牛乳」という商品を20本買ってきて、実際の量を調べたところ平均値\(\overline{X}\)は490mLだった。
この時、この商品は充填量をごまかしていないと言えるか?
※ただし充填に伴うばらつきは標準偏差でσ=30mLであることが分かっているとする。
では実際に解いてみましょう!
①まず帰無仮説を設定する
今回の帰無仮説は、
帰無仮説:
母集団の平均値μは500mLである。
とします。
逆に実際に主張したい対立仮説は、
対立仮説:
母集団の平均値μは500mL未満である。
とします。
②帰無仮説を前提に確率を求める
母集団:平均値μ=500mL,標準偏差σ=30mL
の条件で標本(n=20)の平均値の確率分布を考えます。
この場合の確率分布は、平均値=μ、分散=σ2/nの正規分布に従うことが知られているので、確率分布は下式になります。
標本の平均値の分布(中心極限定理):
\(N(μ,\dfrac{σ^2}{n})=\dfrac{1}{\sqrt{2π\dfrac{σ^2}{n}}}\exp{-\dfrac{(\overline{X}-μ)^2}{2\dfrac{σ^2}{n}}}\)
とりあえずここでは式の意味は理解していなくても、
この式で確率を計算できるということだけ受け入れてもらえればOKです。
結果をグラフであらわすと、下図のようになります。
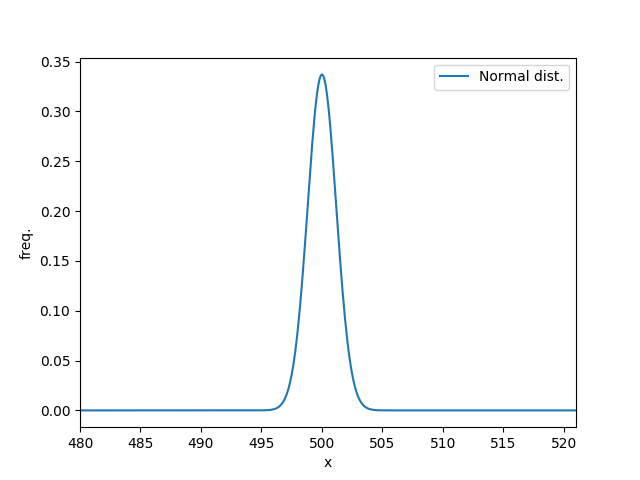
今回は片側検定でいきます。
490mL以下の領域に注目して、p値を求めると、、
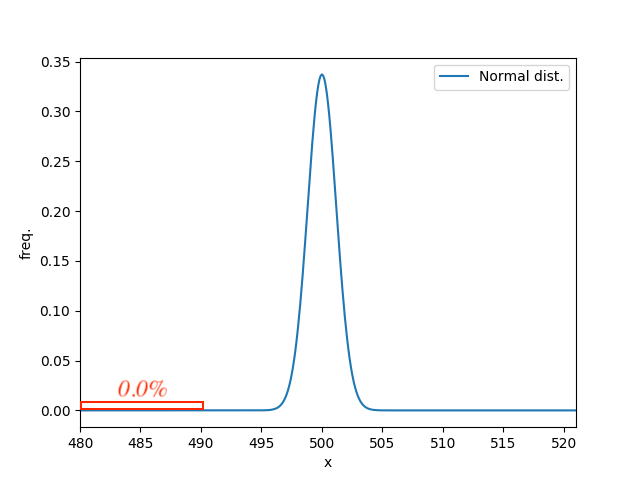
図示するともはや計算するまでもないですが、
p値は0.0%となりました。
③有意水準を設定する
今回は片側検定なので有意水準を2.5%に設定します。
④p値と有意水準を比較する
p値0.0%<有意水準2.5%
であることが確認できました。
⑤結論を出す
よって帰無仮説は棄却され、この商品の平均値は500mLよりも小さそうだとなります。
「誠実牛乳」と言いながら誠実ではなさそうですね。。。
まとめ
今回は仮説検定のやり方について説明しました。
仮説検定は、理系の技術職をやっている人にとっては必須の技術です。
その裏付けとしてなんと2022年には高校数学での必修化が検討されているそうですよ。
社会人の方は高校数学で統計をやっていない人も多いと思いますが、未来の新人に馬鹿にされないように勉強しておきましょう。
実践でもどんどん使っていきましょう!
参考文献
今回の記事を作成するにあたって参考にさせていただきました。
高校数学でわかる統計学 本格的に理解するために (ブルーバックス)











コメントを書く