こんにちは、えびかずきです。
今回はExcelで『t検定』をする方法について解説します。
結論として、
Excelには二標本の標本平均に関するt検定が標準搭載されていて、
①対応のある2標本の場合
②対応のない2標本で母分散が等しいと仮定できる場合
③対応のない2標本で母分散が等しいと仮定できない場合
の3ケースに分類して、t検定を実施できます。
では、具体的に説明していきましょう!
t検定とは
t検定とは、下式のt値がt分布に従うことを利用しておこなう仮説検定です。
\(t≡\dfrac{\overline{X}−μ}{\sqrt{\dfrac{s^2}{n}}}\)
※t分布の意味については別記事で解説していますので、そちらをご参照ください。
(仮説検定をデータ解析に使ってみよう!【t分布の意味編】)
このうちExcelでは、
2標本の平均値の優位差を判断するt検定
の関数や分析ツールが準備されています。
これらにExcelツールがどんな時に使えるかというと、下図に示す通り、
母集団の分散はわからないけど、
標本1と2の平均値の差に意味があるのかを判断したい時に使います。
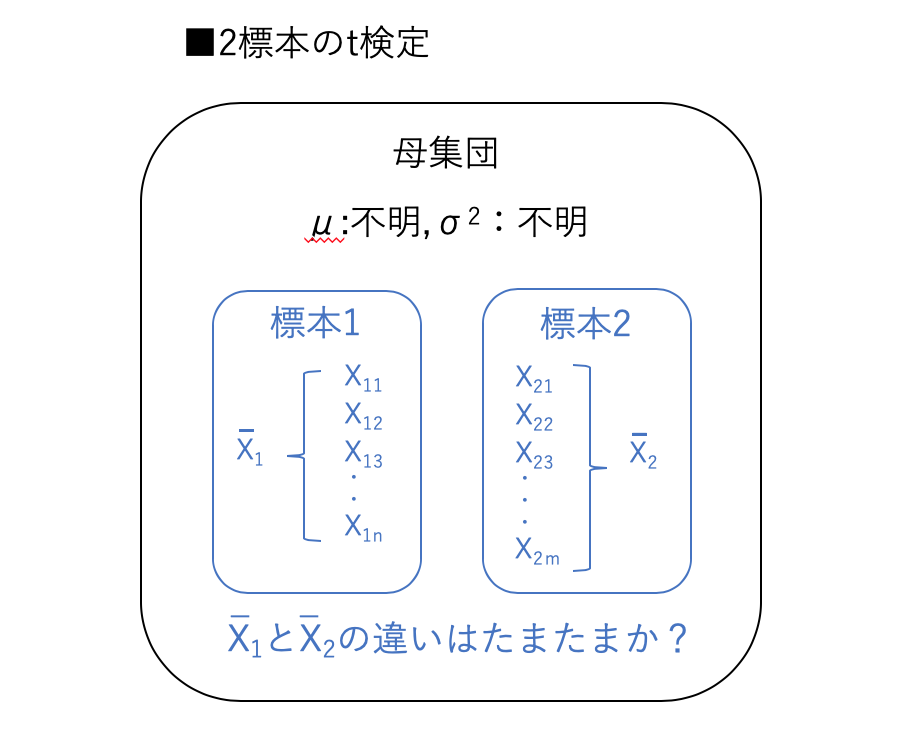
言い換えると、たまたまズレただけかそれとも母集団が違うのかを判断したいということです。
母分散が既知の場合は、Z検定という別の簡単は検定をすればいいのですが、
多くの場合は母分散が不明なこのケースに該当するので、t検定はかなり使用頻度が高いです。
では具体的な使用方法をみていきましょう。
関数T.TESTを使う場合
Excelの公式ガイドには以下の説明があります。
Microsoft Excel
スチューデントの t 検定に関連する確率を返します。
構文
T.TEST(配列1,配列2,検定の指定,検定の種類)
▪ 配列1: には一方のデータ配列を指定します。
▪ 配列2: にはもう一方のデータ配列を指定します。
▪ 検定の指定: には片側検定の場合は 1、両側検定の場合は 2 を指定します。
▪ 検定の種類: には実行する t 検定の種類を指定します。
対応のある検定の場合は 1、2 標本の等分散が仮定できる場合は 2、2 標本が非等分散の場合は 3 を指定します。
要するに、T.TEST()に必要な引数を指定してやれば、P値が返ってきます。
ここでのP値は、
2標本を抽出した母集団の平均値が等しいと仮定した場合に、今データとして得られている以上の2標本の平均値の差が発生する可能性(0~1)のことです。
つまり出てくるP値が小さいほど、母集団の平均値が等しくない、すなわち標本の平均値に有意差があると言えるわけです。
上のExcel公式の説明で使い方を理解できる人は良いのですが、
t検定に慣れていない人はおそらく、「検定の種類」で何を選択すべきかで戸惑ってしまうと思います。
ではそれぞれの意味について順番に説明していきましょう。
①対応のある2標本の場合
まず、対応のある2標本の場合についてです。
これは検定の種類:「対応のある検定の場合は 1」に該当するケースです。
対応のある2標本の場合というのは、
下図のように一つ一つのデータが標本1,2で一対一対応しているというケースです。
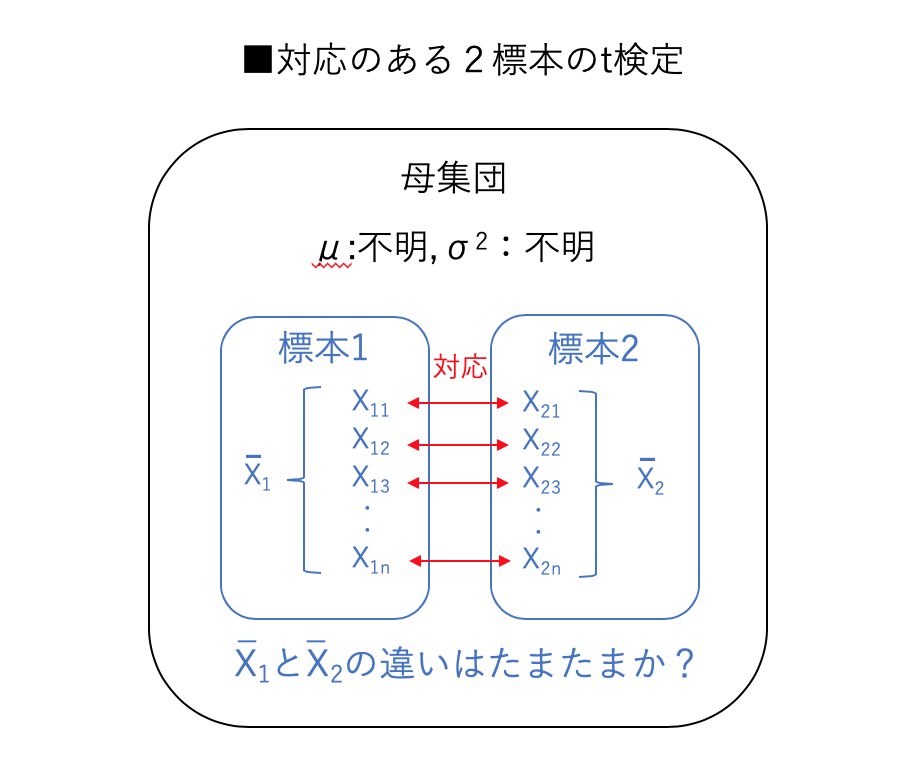
対応のある2標本の場合は、一対一対応しているそれぞれのデータの差(\(d_i=X_{1i}-X_{2i}\))を新たに定義すると、実質的に1標本のt検定に帰結させることができます。
ここで考えるt値は、
\(t≡\dfrac{\overline{d}−μ}{\sqrt{\dfrac{s^2}{n}}}\)
となり、帰無仮説としてμ=0を仮定すると、
\(t≡\dfrac{\overline{d}}{\sqrt{\dfrac{s^2}{n}}}\)
として、t検定を実施することができます。
この説明だとちょっと抽象的でわかりづらいと思いますが、下の使用例をみるとわかりやすいと思います。
使用例
問題:
A〜E君の計5名が、自由に走って50m走のタイムを測ったところ、表中左の結果になりました。
一方で体育の先生が早く走れるフォームを教えてA~Eそれぞれを走らせたところ、表中右の結果となりました。
このとき、早く走れるフォームには効果があったと言えますか?
(※ただし、片側検定の有意水準2.5%で検定を実施するものとする。)
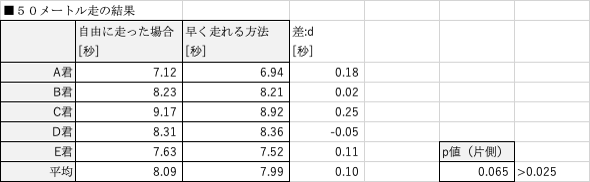
こういった問題を解く場合に、対応のある2標本の検定を使用します。
解き方:
下図のように、T.TEST関数に適切に引数を指定すると、p値が出力されます。
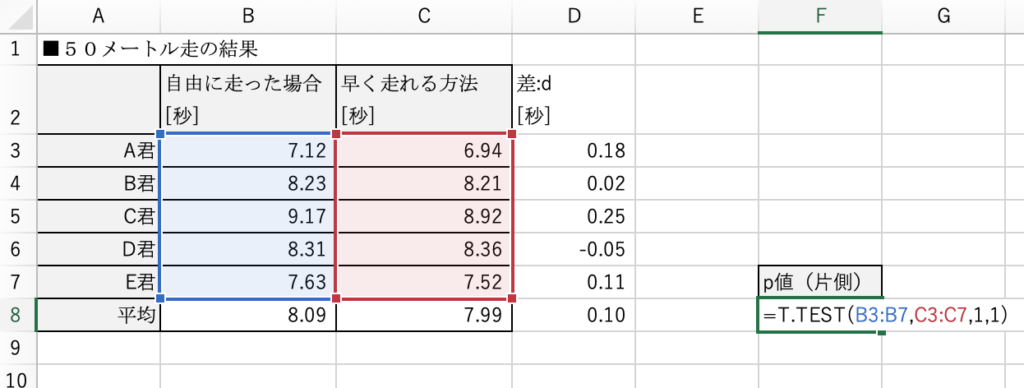
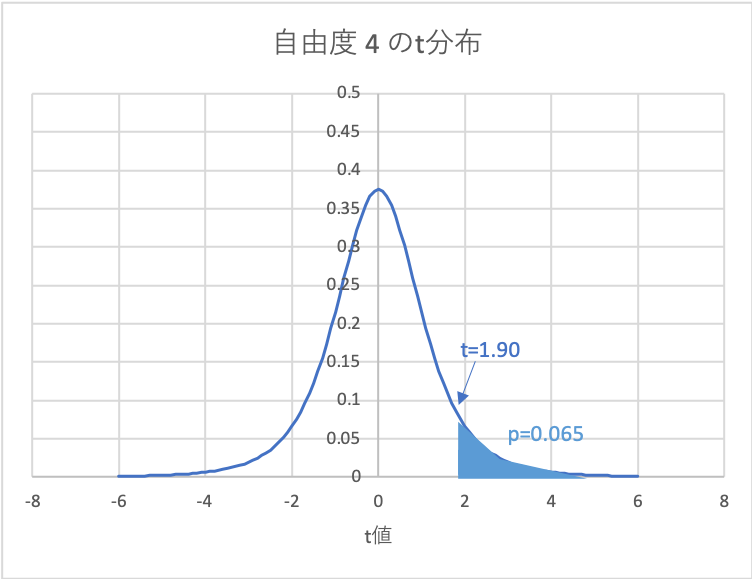
この場合p値は0.065(6.5%)となり有意水準2.5%よりも大きいため、
この結果からは、早く走れるフォームに効果があったとはいえません。
図示すると、以下のようになります。
\(t≡\dfrac{\overline{d}}{\sqrt{\dfrac{s^2}{n}}}=\dfrac{0.10}{\sqrt{\dfrac{0.12^2}{5}}}=1.90\)
※自由度はn-1
②対応のない2標本で母分散が等しいと仮定できる場合
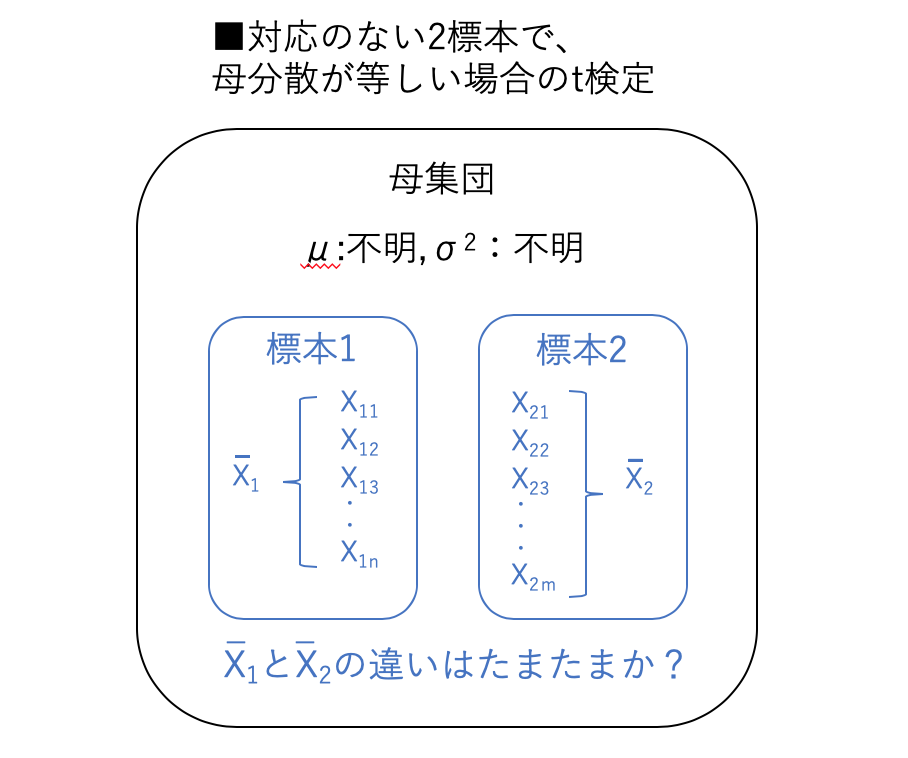
さて続いては、対応のない2標本で母分散が等しいと仮定できる場合です。
つまり検定の種類の「2 標本の等分散が仮定できる場合:2」に該当するケースです。
これは、下図のように標本1、2それぞれの各データが一対一対応になっていないケースです。
この場合は標本1,2で標本サイズが異なっていてもOKです。
(図では標本1のサイズをn、標本2のサイズをmとしています。)
このケースの場合は、
\(t≡\dfrac{(\overline{X_1}-\overline{X_2})-(μ_1-μ_2)}{\sqrt{s^2(\dfrac{1}{n}+\dfrac{1}{m})}}\)
としてt値を考えて、さらに帰無仮説として\(μ_1=μ_2=μ\)と仮定すると、
\(t≡\dfrac{\overline{X_1}-\overline{X_2}}{\sqrt{s^2(\dfrac{1}{n}+\dfrac{1}{m})}}\)
となります。
ただしここでの\(s^2\)は、標本1,2の不偏標本分散(\(s_1^2,s_2^2\))から算出した「プールした分散」を表します。
\(s^2=\dfrac{s_1^2(n-1)+s_2^2(m-1)}{n+m-2}\)
使用例
では具体例をみていきましょう。
問題:
A組5名とB組7名の生徒に同じ数学のテストを受けさせたところ、下表の結果になった。
この結果からA組とB組で学力差があると言えるか?
(※ただし、両側検定の有意水準5.0%で検定を実施するものとする。)
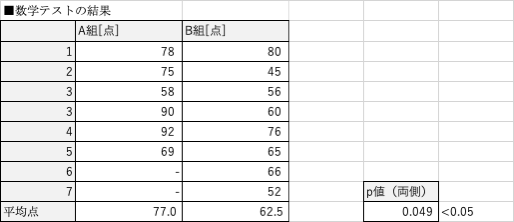
こういった場合に、対応のない2標本で母分散が等しいと仮定できる場合のt検定を適用します。
解き方:
下図のように、T.TEST関数に適切に引数を指定すると、p値が出力されます。
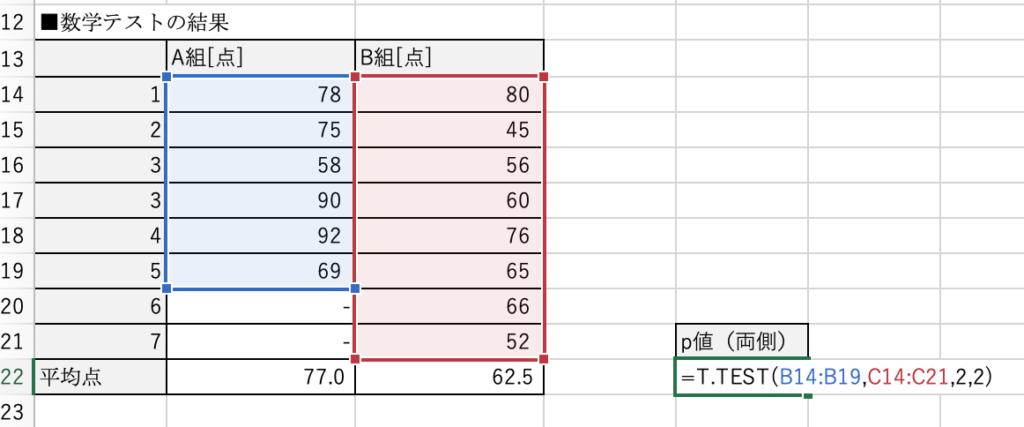
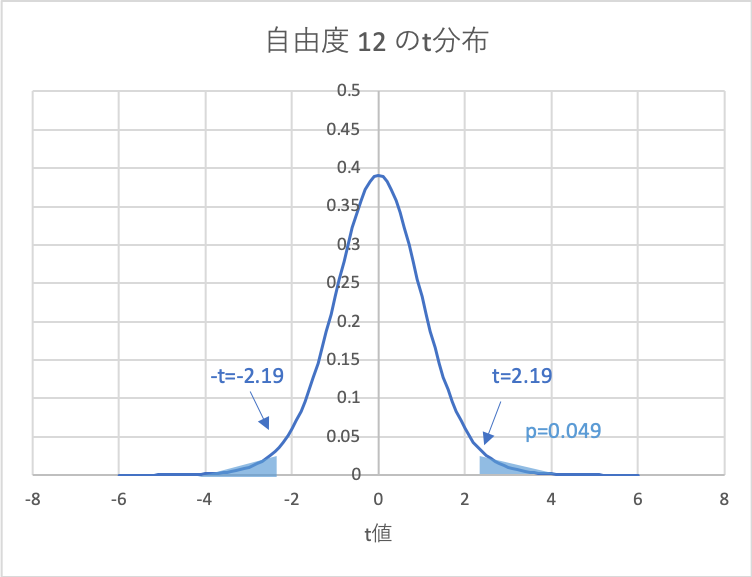
この場合、p値は0.049(4.9%)となり有意水準5.0%よりも小さいため、
A組とB組には学力差があるといえます。
図示すると、以下のようになります。
\(t≡\dfrac{\overline{X_1}-\overline{X_2}}{\sqrt{s^2(\dfrac{1}{n}+\dfrac{1}{m})}}=\dfrac{77.0-62.5}{\sqrt{149.67(\dfrac{1}{6}+\dfrac{1}{8})}}=2.19\)
※自由度はn+m-2
③対応のない2標本で母分散が等しいと仮定できない場合
さて最後に、対応のない2標本で母分散が等しいと仮定できない場合です。
つまり検定の種類の「2 標本が非等分散の場合:3」に該当するケースです。

このケースではウェルチのt検定という特別な手法を使います。
t_0として、
\(t_0 = \dfrac{| \overline{x}_1 – \overline{x}_2 |}
{\sqrt{\dfrac{s_1^2}{n} + \dfrac{s_2^2}{m}}}\)
を考え、さらに自由度fを、
\(f\fallingdotseq\dfrac{\left( \dfrac{s_1^2}{n} + \dfrac{s_2^2}{m} \right)^2}
{\dfrac{ \left( \dfrac{s_1^2}{n} \right)^2}{n – 1} +
\dfrac{\left( \dfrac{s_2^2}{m}\right)^2}{m – 1}}\)
と近似して、t値がt分布に従うと仮定します。
これを理解するのは難易度が高いですが、この手法は要するに母集団の分散が違っていても自由度でなんとかちょうじりを合わせて検定しようというものです。
使用例
では具体例をみていきましょう。
問題:
パン屋A店とB店はチェーン店で、同じフランスパンを作っている。
無作為にそれぞれのお店で製造したフランスパンの重さを測定してみたところ以下のような結果を得た。
お店の特徴として、B店の店員はA店の店員より操作が雑で、重さのばらつきが大きい。
このとき、A店とB店のフランスパンの重さの平均値に差はありそうか?
(※ただし、両側検定の有意水準5.0%で検定を実施するものとする。)
こういった場合に「2 標本の非等分散の場合:3」を使います。
解き方:
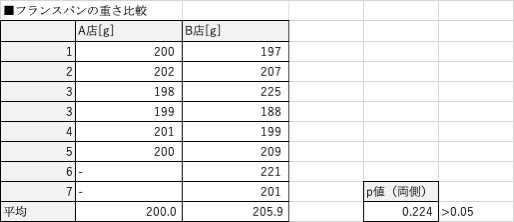
下図のように、T.TEST関数に適切に引数を指定すると、p値が出力されます。
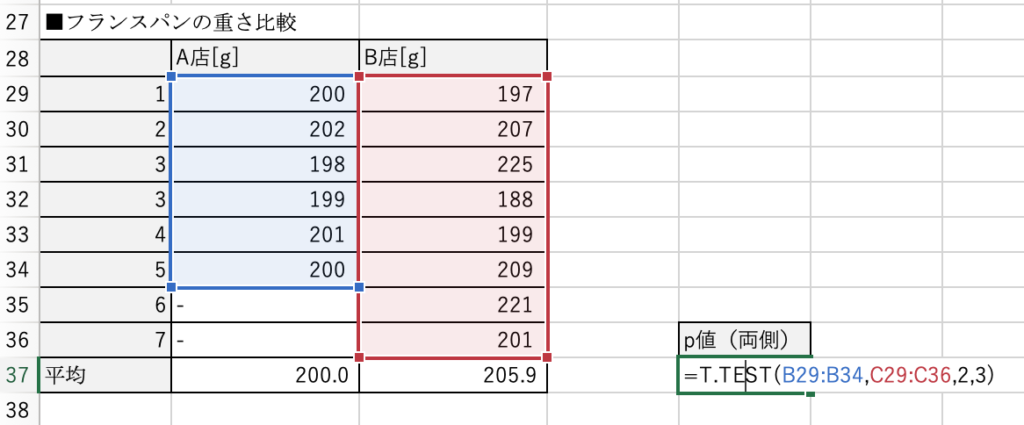
この場合、p値は0.224(22.4%)となり有意水準5.0%よりも大きいため、
このデータからはA店とB店のフランスパンの重さに差があるとはいえません。
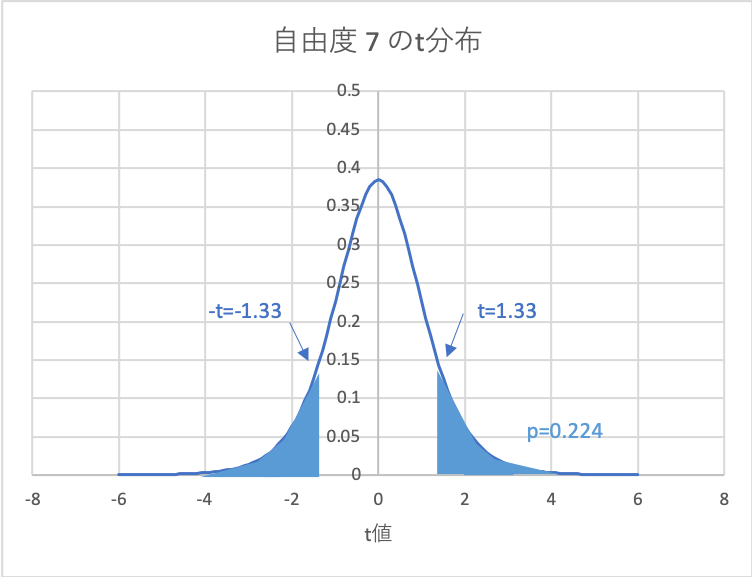
図示すると、以下のようになります。
\(t = \dfrac{| \overline{x}_1 – \overline{x}_2 |}
{\sqrt{\dfrac{s_1^2}{n} + \dfrac{s_2^2}{m}}}=\dfrac{| 200.0 – 205.9 |}
{\sqrt{\dfrac{1.41^2}{6} + \dfrac{12.39^2}{8}}}=1.33\)
※自由度は7(ウェルチのt検定による)
分析ツールを使う場合
関数以外にも分析ツールを使う方法があります。
分析ツールはエクセルの「データ」→「データ分析」から開くことができます。
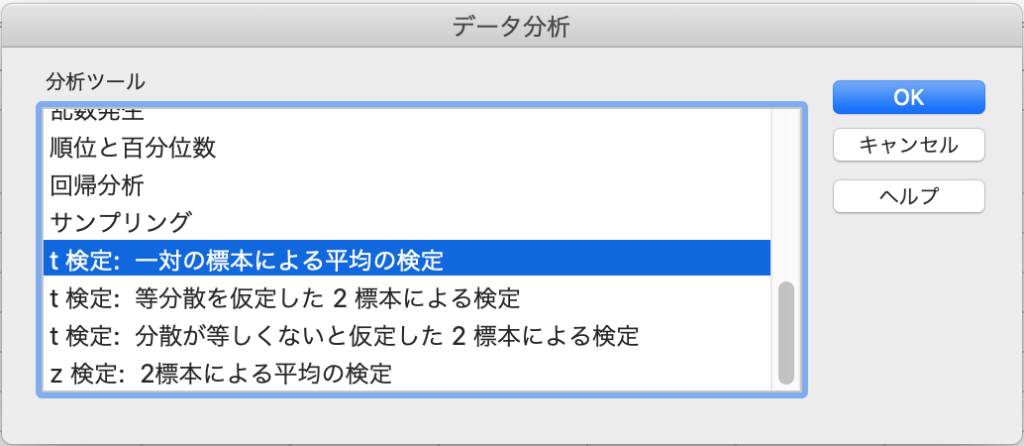
分析ツールでもやはり上で説明した、3パターンを選べるようになっています。
t.test関数を使うときと同様に、適切なものを選びましょう。
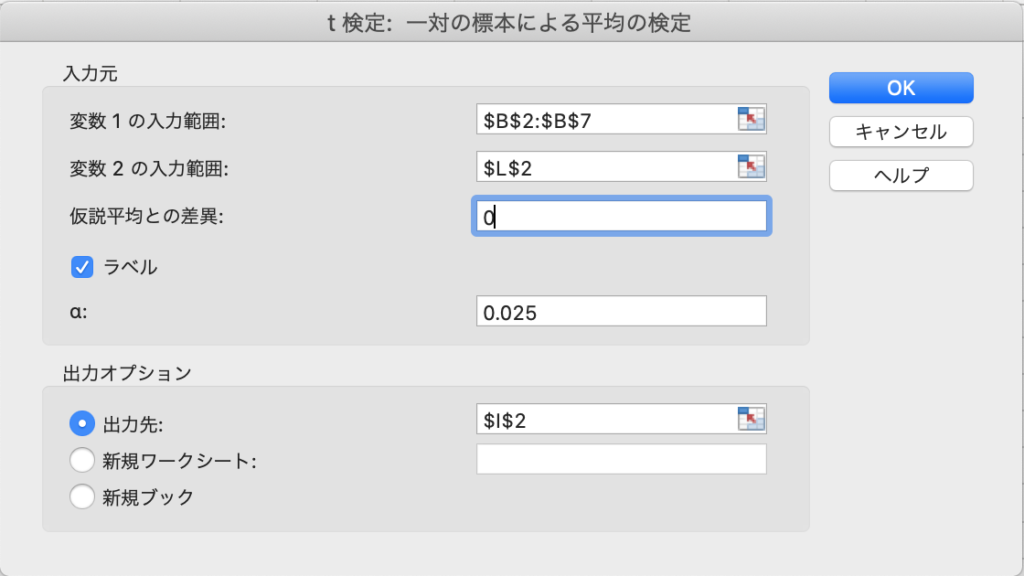
設定画面に必要セルを指定して、OKを押せば、
結果が指定したセルに記載されます。
※分析ツールでは「仮説平均との差異」を指定できます。
ここには普通、母平均が等しいことを仮定する0を入れますが、例えば1といれると母平均が標本1と標本2で1ずれている場合の帰無仮説をたてることになります。
これを指定できる分だけ、分析ツールは若干用途が広がります。
結果例
分析ツールを使って、t.test関数で実施したのと同じt検定をやってみましょう。
結果は以下のとおりです。
結果例(①対応のある2標本の場合)
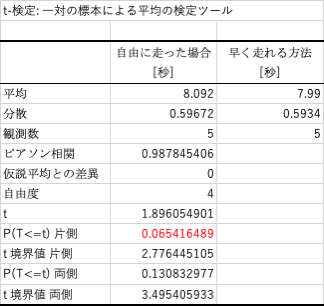
結果例(②対応のない2標本で母分散が等しいと仮定できる場合)
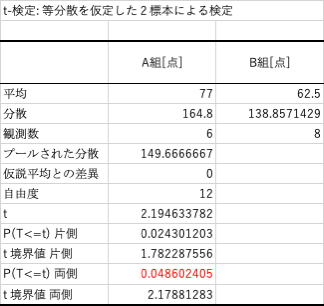
結果例(③対応のない2標本で母分散が等しいと仮定できない場合)
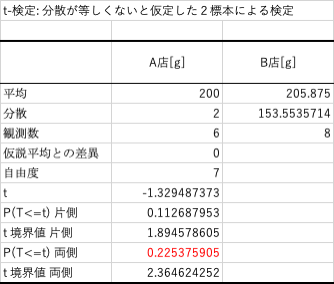
それぞれt.test関数をつかったときと同様の結果が得られていますね。
まとめ
今回はExcelでt検定をする方法について説明しました。
Excelでt検定をしたいけれど、どれを使えば良いかわからず困っているという方は案外と多いのではないでしょうか?
Web上を見渡してみてもケース別にその意味と使い方を説明している記事はあまりなかったので、この記事をかきました。
t検定は統計分析の中でも使用頻度がかなり高く、パワフルな検定手法なので、
意味をきちんと理解してどんどん使っていきましょう!
参考
いろいろ調べてみたところ『統計Web』さんが二標本のt検定についてわかりやすく解説していたので、リンクを貼ります。
統計Web:
https://bellcurve.jp/statistics/course/9427.html
t.test関数のExcel公式サポート:






コメントを書く