Maximaの数式をエクセルへ移植する方法
今回はMaximaで得られた数式をそのままエクセルへ移植して使う方法についてご説明したいと思います!
手順の概要
流れとしては、Maximaに表示される数式をコピー→エクセルのセルへペースト→係数を”名前の定義”で設定(→必要に応じて関数の設定)となります。
では今回は簡単な例として、Maximaで得た二次関数の解をそのままエクセルで使う手順について順を追って説明します。
①数式の準備
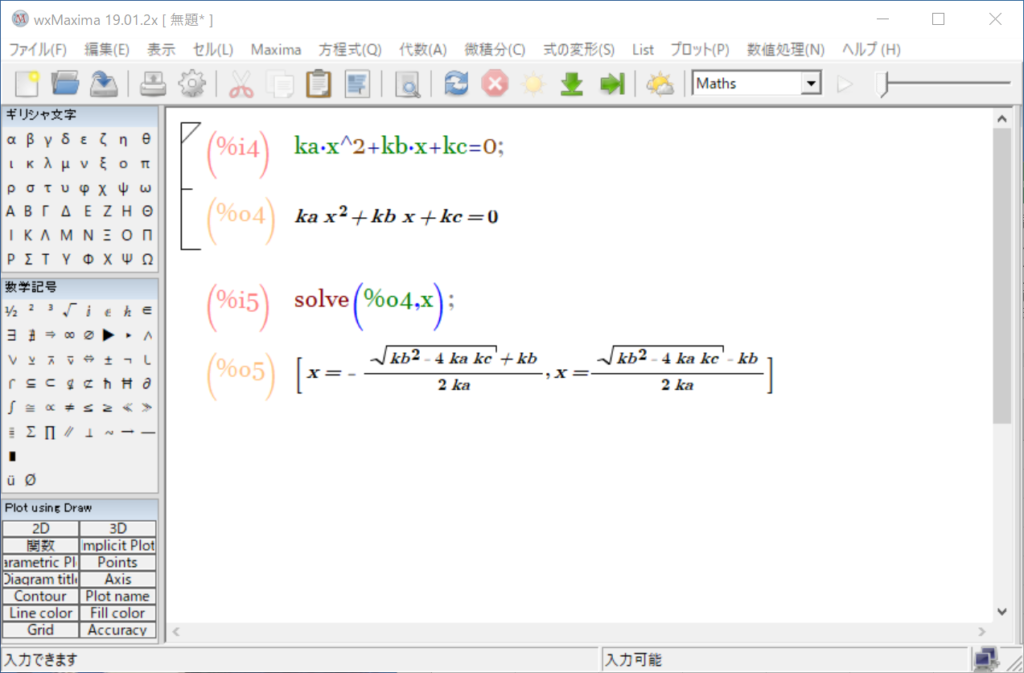
まず上図の様にMaximaに二次方程式を解かせて解の公式の数式を得ます。
(今回は係数をka,kb,kcとしています。エクセルでの取り扱いの都合上この様な係数としていますが、その意味は後で説明します。)
②エクセルの準備
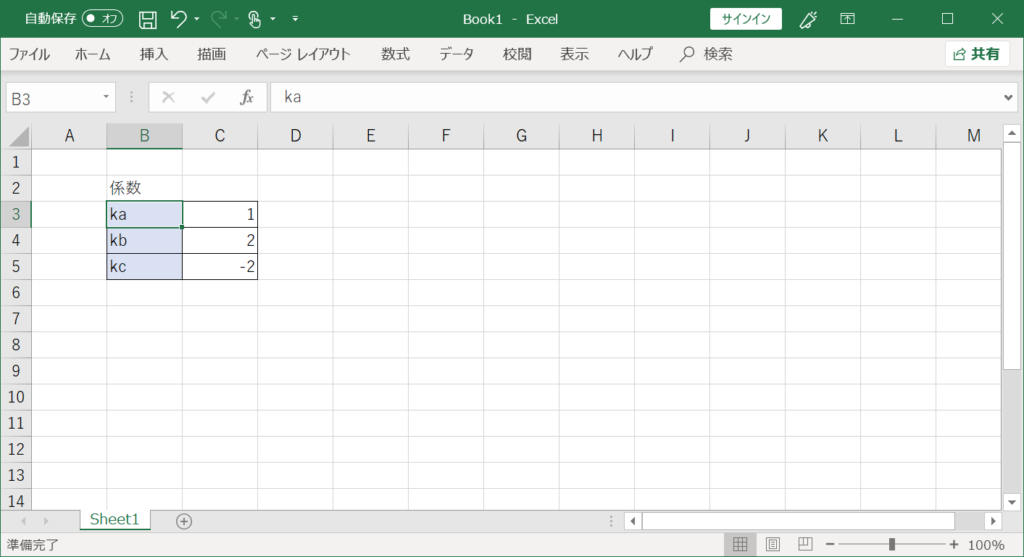
上図のように移植したいエクセルシートへ係数の値を入力するセルを作成します。
今回の場合は、ka,kb,kcの三箇所になります。
③名前の定義
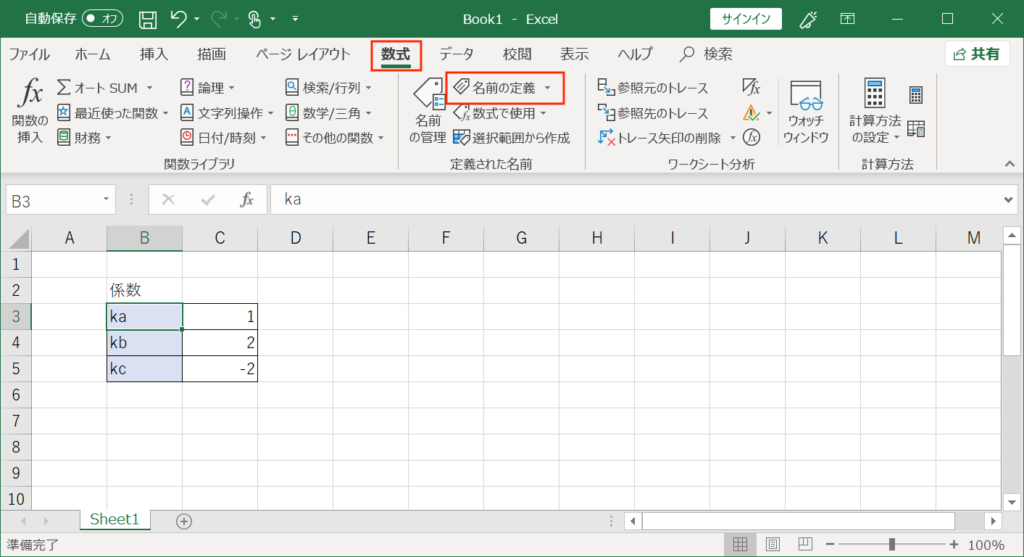
Maximaの数式と対応させるために、セルの名前を定義してやります。「数式」タブの「名前の定義」という項目をクリックします。
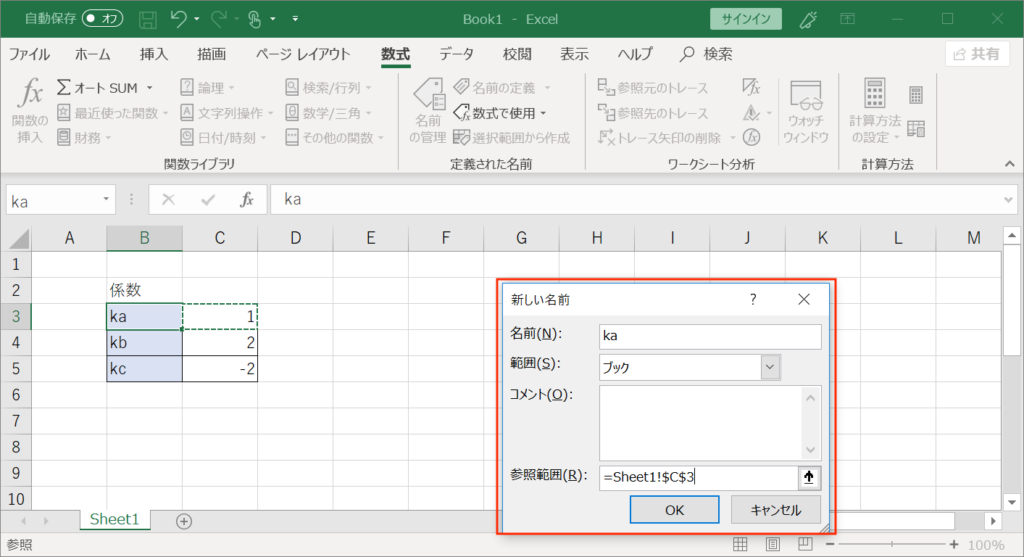
すると、上図のような入力ボックスが出てくるので、係数の値を入力しているセルの名前を、Maximaで使用した係数の名前そのものとしてやります。
今回のケースであれば、
- C3→ka
- C4→kb
- C5→kc
となります。
注意:
「名前の定義」で指定できる名前には制限があり、一文字のアルファベット「c,C」「r,R」は使用することができません。
この制限があるため今回は二次方程式の係数を「a,b,c(←使えない)」とはせず、あえて「ka,kb,kc」としました。
また、「A1,B5,AA10」のようなセル番地と同じ名前は使用することができません。その他の細かい制限については例えばこちらのExcel2010:名前に使える文字・使えない文字などにまとめられていますのでご参照ください。
数式のコピー&ペースト
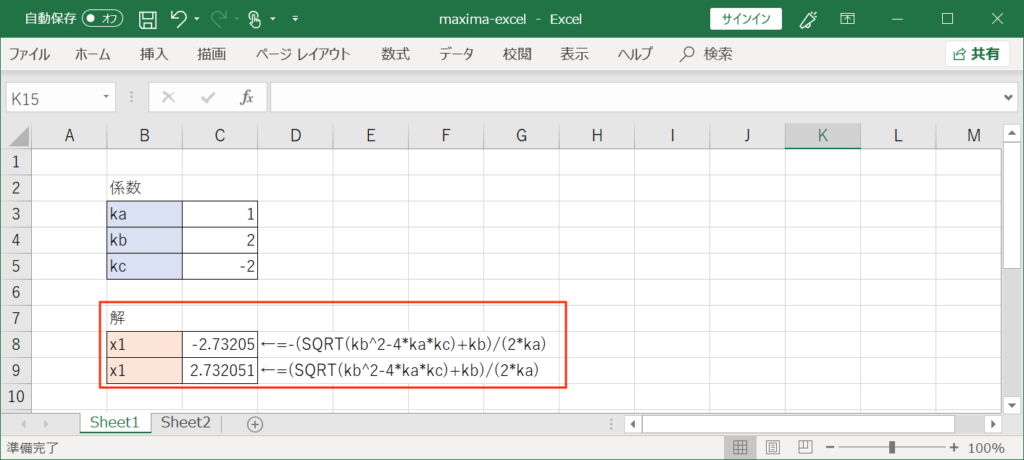
Maximaの数式を直接コピーしてエクセルへ貼り付けます。
今回は二次方程式の解なので入力セルを2つ用意して、それぞれ赤枠のように貼り付けました。
すると、解が演算されて結果が表示されます。
虚数の取り扱いについて
実数の取り扱いのみで良ければ、上の手順まででOKです。
ですが虚数の演算も実施したい場合は、もう少し工夫してやる必要があります。ここではその手順について説明します。
※ちなみに上までの手順で解が虚数になる係数を指定すると、エクセルは虚数の演算ができず「#NUM!」というエラーセルとなってしまいます。
①実部と虚部に分ける
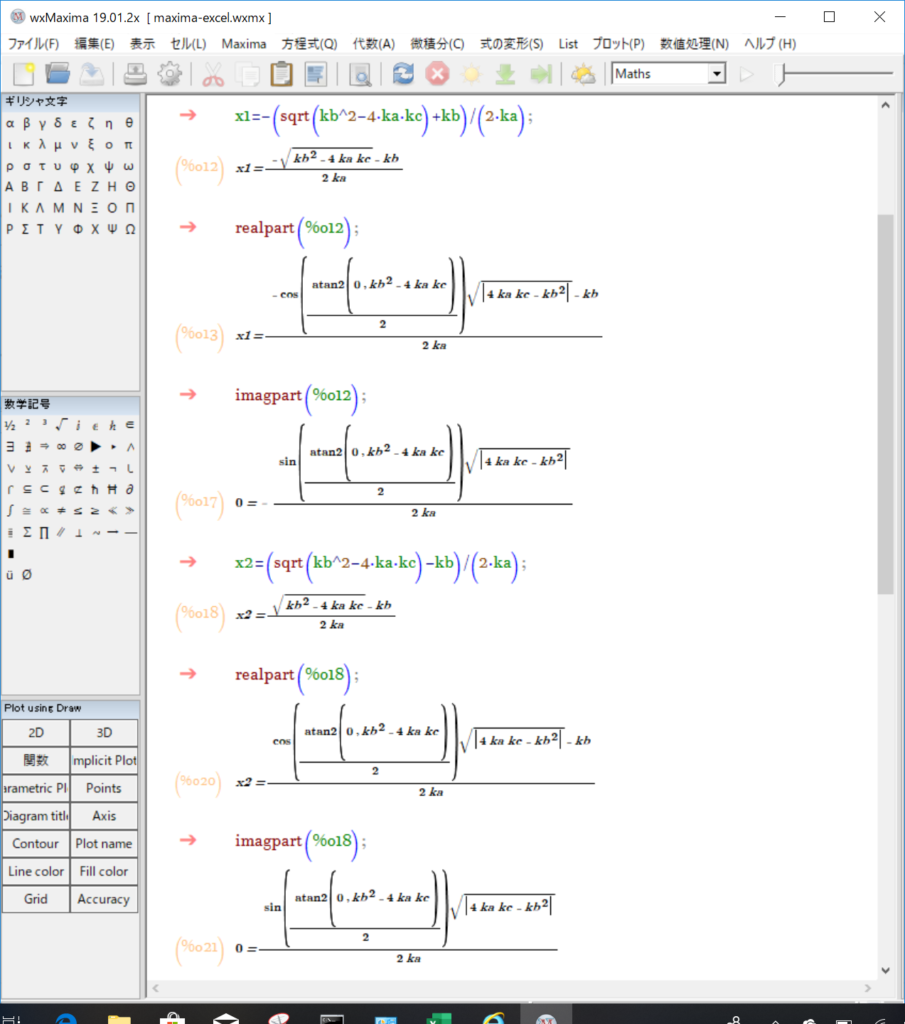
下準備として、上図のように解の数式を実部と虚部に分けてやります。
Maximaでの操作としては、
- 実部の取り出し→realpart(数式);
- 虚部の取り出し→imagpart(数式);
とすればOKです。
数式のコピー&ペースト
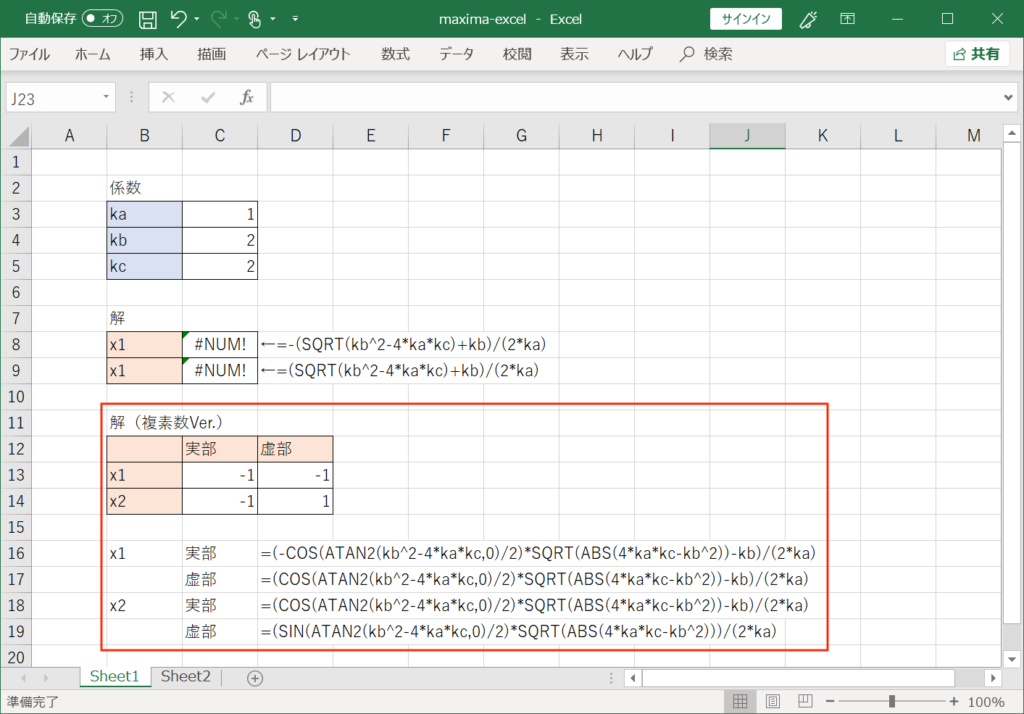
上図のように、実部と虚部それぞれを入力するセルを準備してやり、Maximaの数式をコピー&ペーストしてやります。
これで、虚数の解もエクセルで演算できるようになりました!
注意:
今回の処理でMaximaの結果に出てきたATAN2(y,x)という関数は、エクセルにもあるのでそのまま使えるのですが、惜しいことにエクセルではATAN2(x,y)と、Maximaとはxとyが逆になっているので、これを修正してxとyの位置を交換してやる必要があります。
今回は手作業でエクセル内の式を修正しました。
三次方程式の解をエクセルへ移植する【実践編】
上の例では二次方程式の解をエクセルへ移植しましたが、二次方程式の解の公式はそんなに長い数式ではないのであまり今回の移植方法のありがたみを感じることができないでしょう。
ということで次は、実践編として三次方程式の解をエクセルへ移植してみます!
①数式の準備
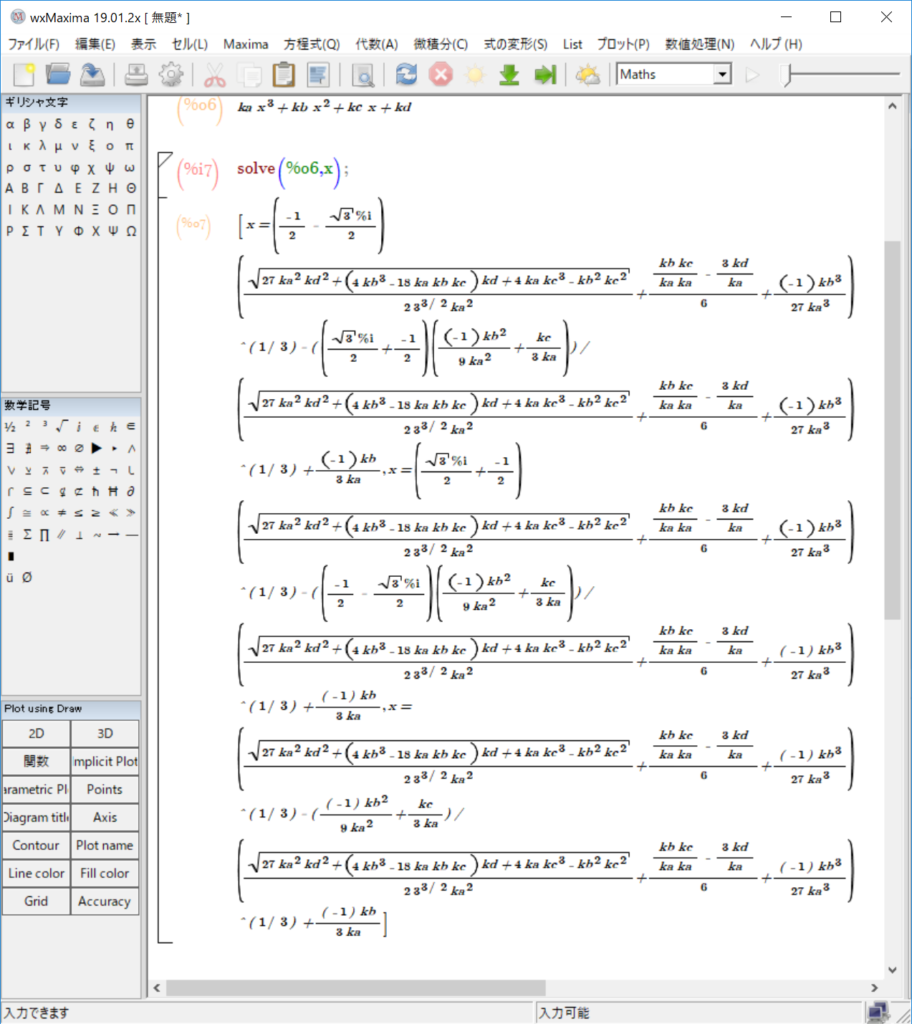
三次方程式の係数を「ka,kb,kc,kd」として、上のようにMaximaで解の数式を求めてやります。
三次方程式の解は「カルダノの公式」として知られていますが、上図に表示されている通り、かなり長い数式となっています。
ここまで来ればさすがに手計算で解を求めようとは思わないでしょう。これをエクセルへ移植します。
②数式の移植
数式の移植方法としては、二次方程式の解の移植で実施した手順と同じように、きちんと「名前の定義」を行なって実施します。
ただ、このカルダノの公式は、公式の段階で既に複素数の形となっているので、上述したように、解を「実部」と「虚部」に分けてから、エクセルへペーストします。
すると、
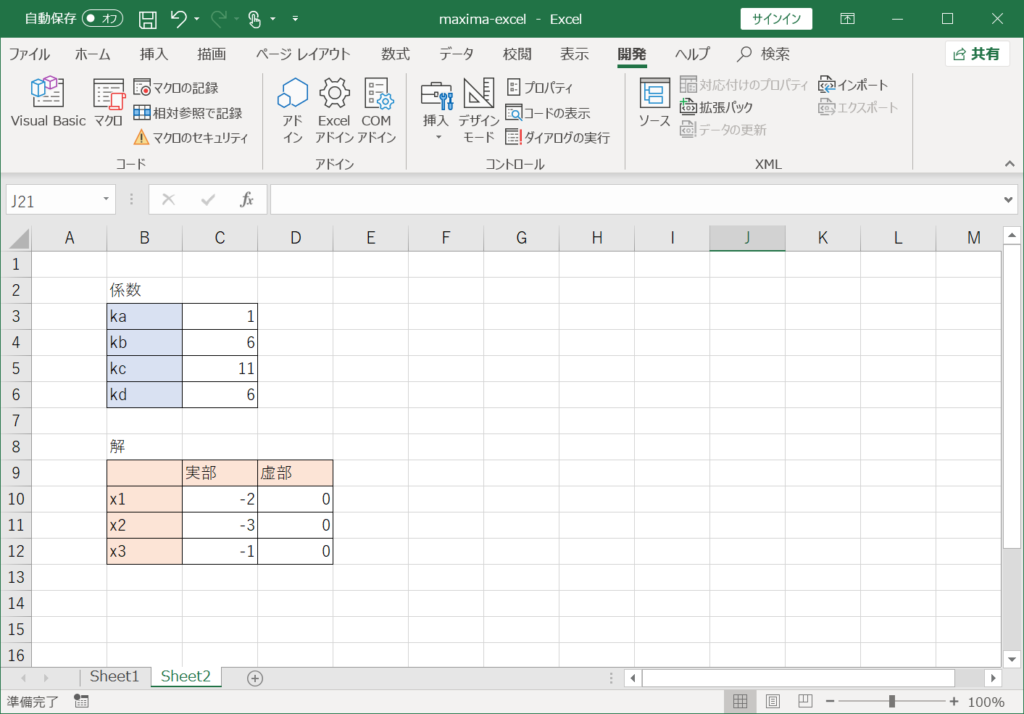
上図のように三次方程式の3つの解が実部と虚部に分かれて結果が表示されました。
これでエクセルで三次方程式の解を演算できるようになりました!
上の図では実数解となる係数条件を指定したため、虚部が全て「0」となっていますが、虚数解となるように係数条件を指定してやると、、、
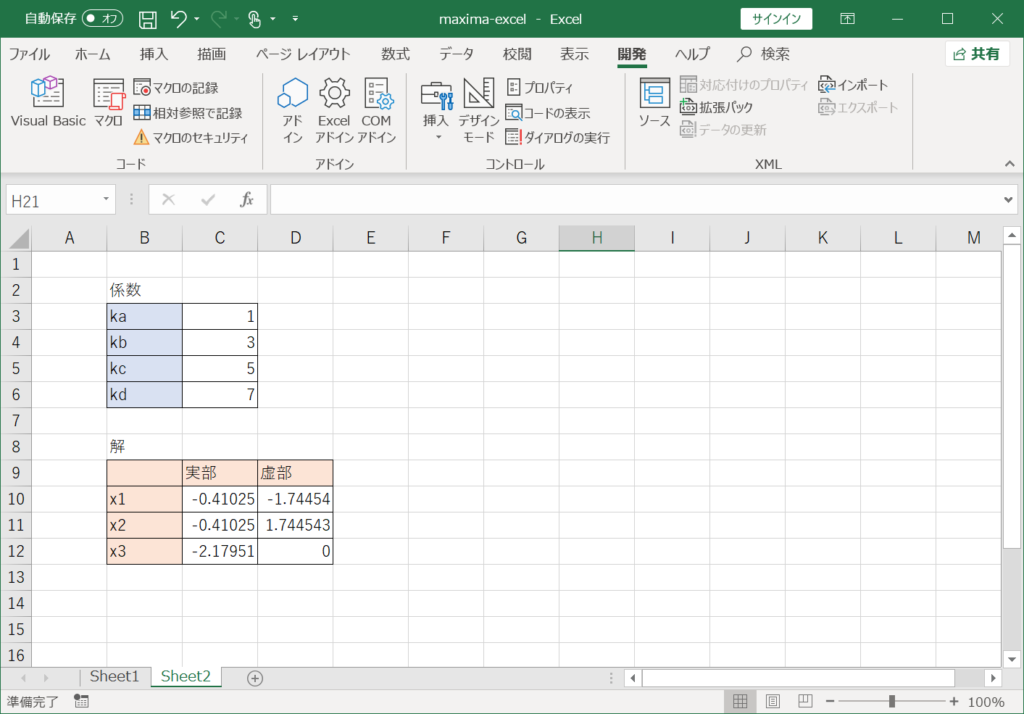
このように、きちんと虚部にも「0」以外の結果が表示され、解を計算することが出来ています。
セルの中身
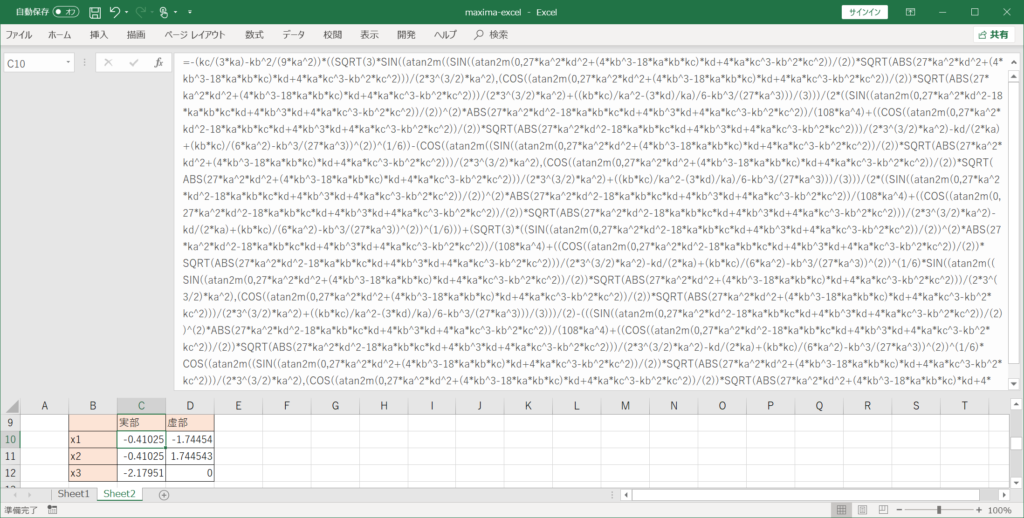
具体的なセルの中身は上のように、途方も無いほど長い数式となっています。これは到底手入力では出来ない量です。
説明した手順を使って是非、Maximaからエクセルへの移植を試してみてください。
補足:
今回の二次方程式の解の時と同じようにATAN2(x,y)関数が解の中に含まれていますので、エクセルに対応させるようにATAN2(x,y)関数のxとyの位置を交換して修正しました。
ただし今回の数式は手作業で修正できないほどに長いものですので、「VBAのユーザー定義関数」の機能と「検索と置換」の機能とを併用して数式修正を実施しました。この方法については機会があれば記事にしようと思います。
三次方程式の解の用途
今回作成した、三次方程式の解を算出するエクセルの用途としては、例えば化学分野での「ファンデルワールス状態方程式」の解の算出に応用することができます。
ファンデルワールス方程式は:
$$p=\frac{RT}{Vm-b}-\frac{a}{Vm^2}$$
(p:圧力、Vm:モル体積、T:温度、R:気体定数、a,b:ファンデルワールス係数)
と表される、気体物質の挙動を説明する状態方程式ですが、
この中のVmを変数とみなすと数式を整理して三次方程式に帰結させることができます。
ある条件におけるVmの数値を求めたい時に、今回得られた三次方程式の解を算出するエクセルファイルが役に立ちます。
この例以外にも三次方程式として表すことができる問題は、世の中に溢れていることでしょう。
まとめ
今回の方法を使えば、Maximaで得られた長い数式をコピペでエクセルに貼り付けて使用することが出来るということがわかりました。
多少関数の修正が必要となる場合もありますが、基本的には「名前の定義」で係数のセル指定をしてやってコピペすることができます。
Maximaで長い数式の結果が得られた時などに、その数式を実用化するためエクセルへの移植を実施してみてはいかがでしょうか!






コメントを書く