こんにちは、えびかずきです。
今回はサイコロを1万回振って、
その結果を統計的に解析してみた結果を紹介します!
こんな人におすすめ:
・サイコロの精度に興味がある
・カイ二乗検定のやり方を勉強したい
実は昔、ネタで「サイコロを1万回振ってみた」という企画をやった事があります。
その時の記事がこちら↓
最近統計学を勉強しているのですが、
ふと、昔サイコロをいっぱい振ったデータがあったなと思い出しました。
この時は統計学の知識が無い状態だったので、せっかく苦労して取ったデータを有効に解析できていません。
これではせっかくのデータがもったいない!と言うことで、
過去記事を抜本的にリライトする形で、データを統計的に解析して考察してみた結果を報告したいと思います。
使ったサイコロ
こんな感じのごく普通のサイコロを、5つ用意しました。
一辺が1cmくらいの小さいサイコロです。近くの玩具屋さんで買いました。

生データ
5つのサイコロを、それぞれ2千回ずつ、合計1万回振ったデータを集めました。
実際にこのデータを集めたのは何年か前の事ですが、相当たいへんだった記憶があります。
なんでこんな事やったんだろう。若気の至りですね。。
結果は下図の通りです。
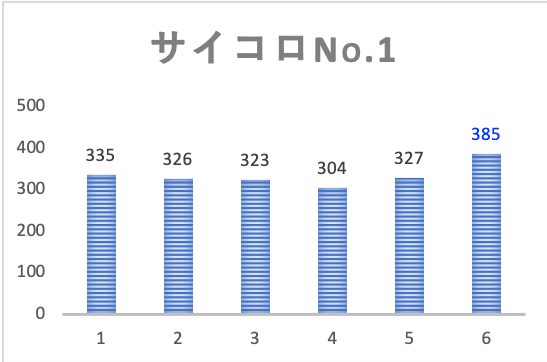
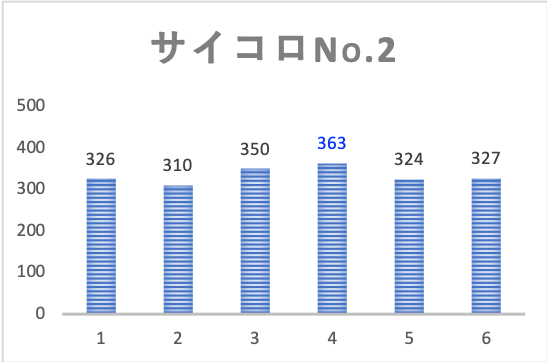
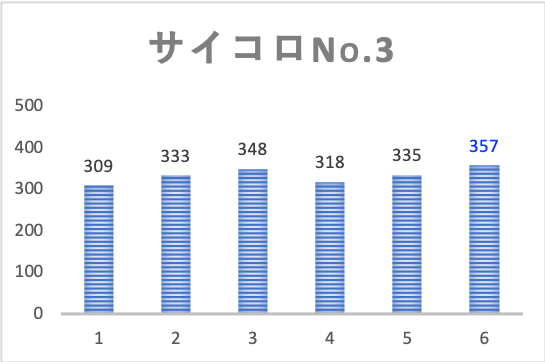
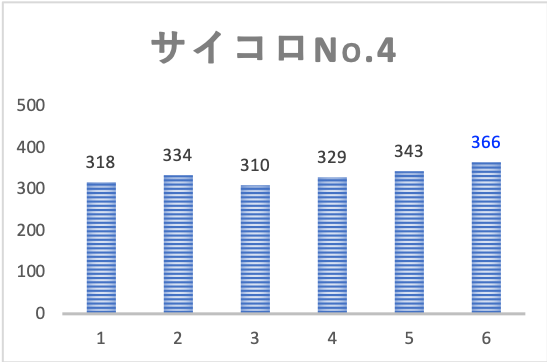
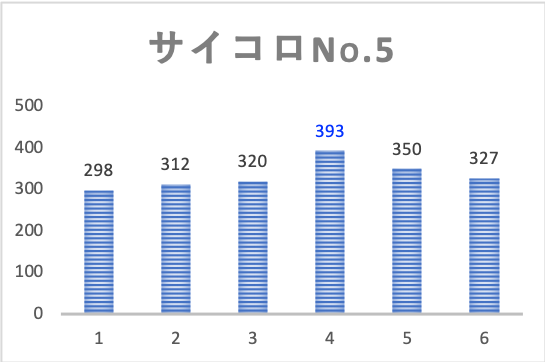
それぞれのサイコロで目の出方にバラつきが見られます。
しかし生データを見ただけだと、これが偶然によるものか、はたまたサイコロ自身の精度によるものなのかは、区別がつきません。
最後に全ての結果をまとめた表がこちらです。
なんとなく目が大きい方が出やすいような傾向がありますが、これは本当でしょうか?
カイ二乗検定とは
このデータをカイ二乗検定で統計的に解析して、
サイコロの目の出方にかたよりが無いかという事を確認してみます。
理論に興味がない人は、ここは飛ばして結果をご覧ください。
カイ二乗検定というのは、下式のような標準正規分布に従う互いに独立な確率変数Xの足し合わせである\(χ^2\)と呼ばれる変数は、必ず\(χ^2\)分布という決まった分布に従う。
ということを利用した仮説検定です。
\(χ^2\)統計量:
\(χ^2=\displaystyle\sum_{i=1}^n X_i^2\)
つまり、これを今回のケースに当てはめた場合、
仮にサイコロの目の出方にかたよりが無いとした場合、それぞれの目の期待度からのズレを足し合わせたものが\(χ^2\)分布に従うはずです。
この仮定の下で計算された\(χ^2\)の確率があまりにも低いのであれば、サイコロにはかたよりがありますねと言える訳です。
自分で書いていても思いますが、ややこしいですね。
この記事の説明だけで理解できる人は、そうとうなセンスをお持ちだと思います。
よくわからない人は、統計Webの記事や統計の教科書を参考にしてみてください。
ちなみに\(χ^2\)分布は下のような形をしています。
検定をするときは、RやPythonやExcelが勝手に計算してくれるので、この式を覚える必要はまったくありません。
\(χ^2\)分布:
\(f(χ^2,m) = \displaystyle\frac{1}{2^{m/2}\displaystyle \Gamma \left(\frac{m}{2}\right)}
χ^{2(m/2-1)}e^{-χ^2/2} \hspace{20px} (0 \leq χ^2 < \infty)\)
※式中のmは自由度を表す
自由度mは、独立な確率変数Xの数で決まります。
要するにXが5個あれば自由度m=5ということです。
今回のケースの場合
今回のケース場合は、下に示す統計量がカイ二乗分布に従います。
上で説明した一般式とは少し形が違いますが、導出は割愛します。
(気が向いたら追って書き加えるか、記事にしますね。このケースではこうなると認めて先に進みましょう。)
\(χ^2\)検定:
\(χ^2=\displaystyle\sum_{i=1}^6 \frac{(O_i-E_i)^2}{E_i}\)
\(O_i\):観測度数,\(E_i\):期待度数
ここで観測度数Oとは、実際に実験で得られたデータのことを意味します。
つまりNo.1サイコロの場合、i(サイコロの目)=1の時の観測度数は335という具合です。
また期待度数Eとは、サイコロの目の出やすさが全て同じとした場合に期待される数のことをいいます。
つまりNo.1サイコロの場合のi(サイコロの目)=1の時の期待度数は全試行の2千を6で割った333.33…になります。
ただしここでの分布の自由度mは、サイコロの目の総数である6ではなく、そこから1を引いた5であることに注意が必要です。
なぜなら、自由度は独立な確率変数の数で決まるからです。
つまり今回のケースの場合、全体の試行回数が決まっているので、サイコロの目5つ分の結果を使えば残りの一つの結果が差し引きで自ずと導かれてしまうので、独立な変数の数は5であるということです。
と言う事で、前置きはここまでにして、実際に計算してみよう!
Pythonでカイ二乗検定をやってみた
統計と言えばRというイメージがありますが、
私はPythonが好きなので今回もPythonで実装していきます。
# 数値計算に使うライブラリ
import numpy as np
import pandas as pd
import scipy as sp
from scipy import stats
# データの読み込み
data = pd.read_csv("no1.csv")
print(data)# output
Oi Ei
0 335 333.333333
1 326 333.333333
2 323 333.333333
3 304 333.333333
4 327 333.333333
5 385 333.333333# カイ二乗検定の実行
Oi=data["Oi"]
Ei=data["Ei"]
sp.stats.chisquare(Oi, Ei)# output
Power_divergenceResult(statistic=11.20000000112, pvalue=0.0475556439440613)こんな感じで、簡単にカイ二乗の値とp値が算出されます。
上の例では、No1のサイコロのみの検定を実行しましたが、他のサイコロ、そしてtotalの結果もまとめたものが下の表になります。
| サイコロNo | χ2 | p値 | 判定(p≦0.05) | 出やすい目 |
| 1 | 11.2 | 0.048 | ○ | 6 |
| 2 | 5.7 | 0.342 | × | – |
| 3 | 4.8 | 0.439 | × | – |
| 4 | 5.9 | 0.318 | × | – |
| 5 | 17.3 | 0.004 | ○ | 4 |
| total | 12.2 | 0.032 | ○ | 6 |
ここでのp値は、サイコロの目の出やすさが全て平等だとした場合に、
\(χ^2\)値が実験結果から得られた値以上の領域に”偶然”入る確率を示しています。
つまりp値が小さければ小さいほど、そもそもの仮定が間違っている可能性が高いということを表しています。
今回の検定では、有意水準を5%として判定をおこないました。
考察
結論として、サイコロNo1と2に関しては、目の出やすさが平等とは言えなさそうです。
どうやら個体差があるようですね。
サイコロが少し歪んでいるのかも知れません。
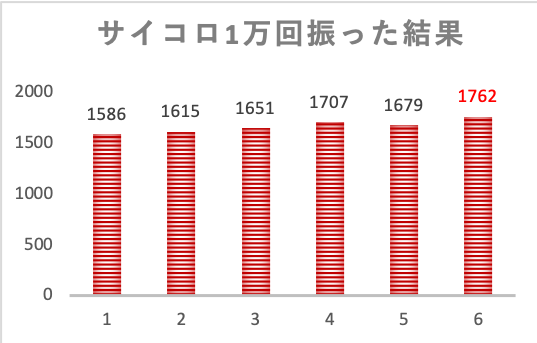
さらに、totalの結果をみてみると、こちらも目の出やすさが平等とは言えなさそうで、6が出やすいという結果になっています。
生データの頻度グラフを見てみると、数字が大きいほど出やすいという結果になっているのが特徴的です。
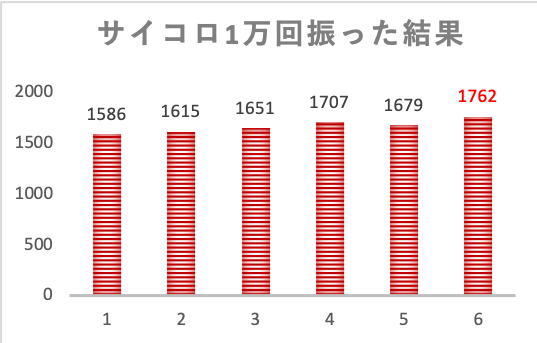
ここから考えられることは、サイコロの個体差とは別に、
数字の数が大きいほど掘りの量が多くて重心が偏っている影響が見えているのでは無いかと言う事です。
どういうことかと言うと、サイコロの表と裏は常に足すと7になるように作られているので、数字の大きい面の下は数字が小さい、すなわち重心が下に偏っている可能性があるということです。
今回はその影響が見えているのかも知れませんね。
まとめ
今回改めてデータを解析してみて、非常に感覚とあう綺麗な結果が出たことにかなり驚きました。
出る目の生データを見て、なんとなく個体差がありそうだとか、全体的に6が出やすそうだなと感覚的に思ってはいましたが、その裏付けとしてカイ二乗検定のp値によって理論的に説明できたので、とても気持ちの良い結果です。
統計を勉強してみて、目から鱗というか、新しい世界が見えてきた感じがするので、これからもどんどん使っていこうと思います。
興味のある方はぜひ試してみてください。
参考文献
初心者向けにかなり易しく説明くれています。
これから統計を学ぼうとする人の一冊目におすすめ。
今回のサイコロのカイ二乗検定の説明もありました。
Pythonで統計分析する時の参考になりました。
こちらも入門書なのでPythonで統計を始めたい人におすすめ。











コメントを書く