こんにちは、えびかずきです。
今回は色々な平均値についてです。
それぞれ名前はきいたことあるけど、意味も使い所もイマイチわからん。。。
という方向けに本質的な意味を理解できるように説明してみました。
結論として、
・相乗平均と調和平均は、関数f(x)のグラフをイメージする。
・対数平均は、積分の平均を考える。
です。
では具体的に説明していきましょう!
いろいろな平均値
平均値には普通の平均の他にいろいろな平均が存在することはご存知ですよね?
代表的なものを並べると以下のようになります。
数値a,bの平均は,
\(相加平均:\dfrac{a+b}{2}\)(普通の平均)
\(調和平均:\dfrac{2}{\dfrac{1}{a}+\dfrac{1}{b}}\)
\(相乗平均:\sqrt{ab}\)
\(対数平均:\dfrac{b-a}{lnb-lna}\)
一般化すると,
\(相加平均:\displaystyle \dfrac{1}{n}\sum_i^nx_i\)
\(調和平均:\displaystyle \dfrac{n}{\sum_i^n\dfrac{1}{x_i}}\)
\(相乗平均:\displaystyle (\prod_i^nx_i)^(1/n)\)
\(対数平均:\dfrac{b-a}{lnb-lna}\)
対数平均は2点間の区間[a,b]のみに定義
※相加平均は算術平均、相乗平均は幾何平均ともいいます。
調和平均と相乗平均の考え方
調和平均と相乗平均は、考え方自体は同じです。
例えば数値aとbの平均値を考える時、
y=f(x)のグラフをイメージして、
「x軸で相加平均(普通の平均)をとったときにyがどうなるか?」を考えます。
下の図を見てもらうと、視覚的にわかりやすいと思います。
調和平均の図示
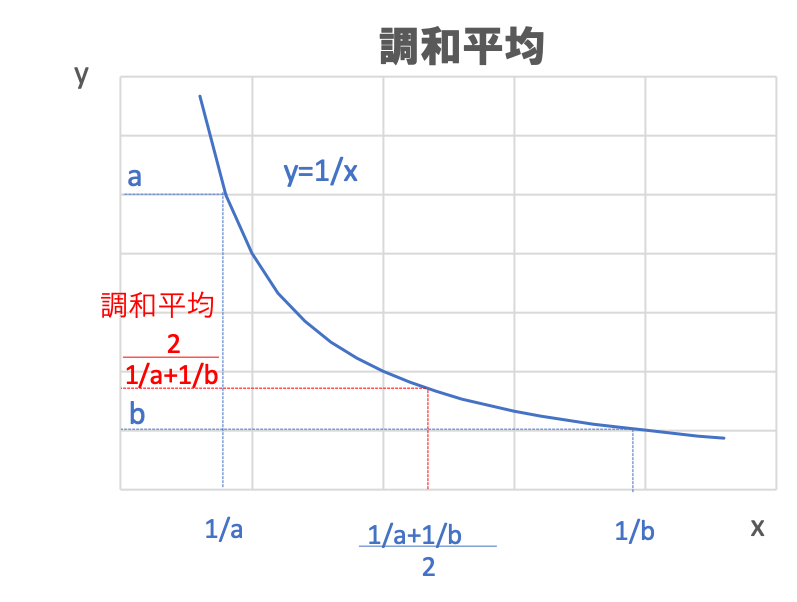
数値a,bの調和平均を具体的に図示すると以下になります。
\(y=1/x\)を考えた場合の、
x軸が相加平均になる時のy軸の値(赤字)が、調和平均になります。
相乗平均の図示
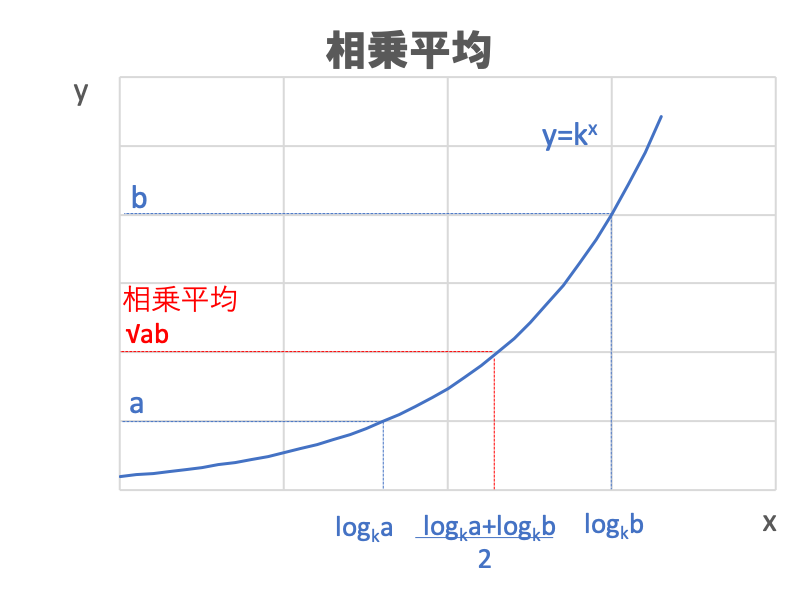
数値a,bの相乗平均を具体的に図示すると以下になります。
\(y=k^x\)を考えた場合の、
x軸が相加平均になる時のy軸の値(赤字)が、相乗平均になります。
数式による説明
調和平均と相乗平均について数式で説明すると以下のようになります。
数値a,bの平均を具体的に数式で示すと、
調和平均、相乗平均の場合:
\(平均値(a,b)=f(\dfrac{f^{-1}(a)+f^{-1}(b)}{2})\)
\(f^{-1}\)は逆関数
となり、
\(調和平均:f(x)=\dfrac{1}{x}, f^{-1}(y)=\dfrac{1}{y}\)
\(相乗平均:f(x)=k^x, f^{-1}(y)=log_{k}y\)
※kは定数、何でも良い。
です。
すでにお気づきと思いますが、
調和平均と相乗平均の違いは考えている関数f(x)の違いです。
言葉で説明するとちょっとわかりにくいですが、図を見ると一目瞭然ですね。
実は、調和平均・相乗平均は、相加平均を含めて一般化平均という種類の平均の仲間であり、
定義となる一つの数式で表すことができます。
詳しくは一般化平均で検索してみてください。
対数平均の考え方
対数平均は、ややこしいですが考え方が他と異なります。
グラフを使って視覚的に説明すると以下のようになります。
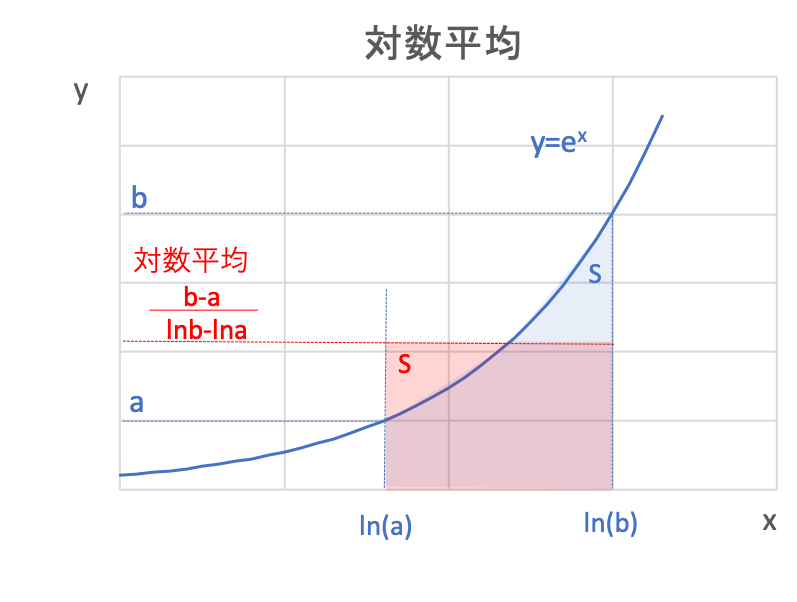
対数平均は、\(y=e^x\)をイメージした時、
上図青色の面積Sと赤色の面積Sが等しくなるようにとったy軸上の赤字で示した値になります。
つまり、\(y=e^x\)をln(a)からln(b)までの区間で積分をした値(S)と、
対数平均×(ln(b)-ln(a))の値(S)が等しくなるようにするということです。
数式で表すと、
\(\displaystyle 対数平均×(ln(b)-ln(a))=\int_{ln(a)}^{ln(b)}e^xdx\)
となり、変形すると、
\(\displaystyle 対数平均=\dfrac{1}{ln(b)-ln(a)}\int_{ln(a)}^{ln(b)}e^xdx\)
\(対数平均=\dfrac{b-a}{ln(b)-ln(a)}\)
となります。
感覚的な説明としては、
ln(a)とln(b)のところに壁を立てて、青色の面積の部分が液体に変わった時に平らになった液面の高さが対数平均ということができます。
これは連続分布の相加平均と呼ばれるものの仲間で、調和平均や相乗平均とは根本的に考え方が違います。
注意:
対数平均は必ず区間[a,b]に対して算出します。
つまり3つ以上の数値に対する平均は定義されていません。
それぞれの用途
調和平均の用途:
平均速さの計算に使えます。
例えば、
家から120km先に職場があります。行きは60km/h、帰りは40km/hで移動したので合計5時間かかりました。この時の平均速度はいくらか?
などがあります。
感覚的に50km/hと答えてしまいそうですが、往復にかかる時間に着目すると、240km/(50km/h)=4.8hとなって、なんか変ですね。
正解は、調和平均をとって2/(1/60+1/40)=48km/hとするのが妥当です。
相乗平均の用途:
指数関数的に増えたり減ったりする数値の計算へ応用できます。
例えば、
当ブログ、エビワークスのPV数(ページの閲覧数)が下の伸び率で順調に増えています。
1月:先月の1.70倍
2月:先月の1.50倍
※数字は架空
未来のPV数を予想するための平均伸び率を考える場合、いくらとするのが妥当か?
正解:√1.70*1.50 = 1.597倍
対数平均の用途:
化学工学での伝熱計算への応用がもっとも有名だと思います。
入口と出口で熱媒との温度差が異なる条件における熱交換器の熱量計算に使えます。
下の記事などが参考になりそうでした。
まとめ
今回は調和平均・相乗平均・対数平均についてその本質について詳しく説明しました。
これらの平均値は普段の生活ではあまり馴染みのないものですが、
理系の学生や技術職の方にとっては避けて通れないものです。
これまでなんとなくで使っていた人はもやもやが晴れたのではないでしょうか?
いろんな平均値を使いこなして、仕事の質を高めていきましょう!
今回は以上です!
参考
今回はWikipediaが参考になりました。




コメントを書く